题目内容
在边长为a的正方形ABCD内随机取一点P,则∠APB>90°的概率是
.
| π |
| 8 |
| π |
| 8 |
分析:点P在正方形ABCD内,若使∠APB>90°,则P应在以AB为直径的半圆内部,所以使∠APB>90°的概率是半圆的面积比上正方形的面积.
解答:解:如图,

在边长为a的正方形ABCD内随机取一点P,
如果P点位于以AB为直径的半圆内部,则∠APB>90°,
否则,若P点位于半圆上及阴影部分,则∠APB≤90°,
所以,∠APB>90°的概率p=
=
.
故答案为
.

在边长为a的正方形ABCD内随机取一点P,
如果P点位于以AB为直径的半圆内部,则∠APB>90°,
否则,若P点位于半圆上及阴影部分,则∠APB≤90°,
所以,∠APB>90°的概率p=
| ||||
| a2 |
| π |
| 8 |
故答案为
| π |
| 8 |
点评:本题考查了几何概型,注意该题的测度比是面积比,同时考查了直径所对的圆周角是直角,此题为中低档题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
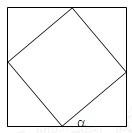 在边长为a的正方形ABCD中内依次作内接正方形AiBiCiDi(i=1,2,3,…),使内接正方形与相邻前一个正方形的一边夹角为a,求所有正方形的面积之和.
在边长为a的正方形ABCD中内依次作内接正方形AiBiCiDi(i=1,2,3,…),使内接正方形与相邻前一个正方形的一边夹角为a,求所有正方形的面积之和. 如图所示,在边长为a的正方形组成的网格中,设椭圆C1、C2、C3的离心率分别为e1、e2、e3,则e1、e2、e3的关系为
如图所示,在边长为a的正方形组成的网格中,设椭圆C1、C2、C3的离心率分别为e1、e2、e3,则e1、e2、e3的关系为 (2013•海淀区二模)如图,在边长为a的正方形内有不规则图形Ω.向正方形内随机撒豆子,若撒在图形Ω内和正方形内的豆子数分别为m,n,则图形Ω面积的估计值为( )
(2013•海淀区二模)如图,在边长为a的正方形内有不规则图形Ω.向正方形内随机撒豆子,若撒在图形Ω内和正方形内的豆子数分别为m,n,则图形Ω面积的估计值为( ) 在边长为a的正方形ABCD中内依次作内接正方形AiBiCiDi(i=1,2,3,…),使内接正方形与相邻前一个正方形的一边夹角为a,求所有正方形的面积之和.
在边长为a的正方形ABCD中内依次作内接正方形AiBiCiDi(i=1,2,3,…),使内接正方形与相邻前一个正方形的一边夹角为a,求所有正方形的面积之和.