题目内容
 在边长为a的正方形ABCD中内依次作内接正方形AiBiCiDi(i=1,2,3,…),使内接正方形与相邻前一个正方形的一边夹角为a,求所有正方形的面积之和.
在边长为a的正方形ABCD中内依次作内接正方形AiBiCiDi(i=1,2,3,…),使内接正方形与相邻前一个正方形的一边夹角为a,求所有正方形的面积之和.
解:令第k个正方形的边长为ak,则ak+1(sina+cosa)=ak (0<a< ),
), =
=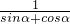
∴( )2=(
)2=(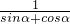 )2,
)2,
即{ak2}为等比数列,且公比小于1,
∴所有正方形面积之和
S= =
= =
=
分析:令第k个正方形的边长为ak,则可表示出ak+1和ak的关系式,整理求得( )2=(
)2=(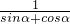 )2,推断出{ak2}为等比数列,进而利用等比数列的求和公式和等比数列的极限公式求得所有正方形面积之和.
)2,推断出{ak2}为等比数列,进而利用等比数列的求和公式和等比数列的极限公式求得所有正方形面积之和.
点评:本题主要考查了数列的应用,数列与极限的综合.考查了学生分析问题和解决问题的能力.
 ),
), =
=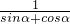
∴(
 )2=(
)2=(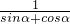 )2,
)2,即{ak2}为等比数列,且公比小于1,
∴所有正方形面积之和
S=
 =
= =
=
分析:令第k个正方形的边长为ak,则可表示出ak+1和ak的关系式,整理求得(
 )2=(
)2=(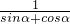 )2,推断出{ak2}为等比数列,进而利用等比数列的求和公式和等比数列的极限公式求得所有正方形面积之和.
)2,推断出{ak2}为等比数列,进而利用等比数列的求和公式和等比数列的极限公式求得所有正方形面积之和.点评:本题主要考查了数列的应用,数列与极限的综合.考查了学生分析问题和解决问题的能力.

练习册系列答案
相关题目
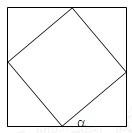 在边长为a的正方形ABCD中内依次作内接正方形AiBiCiDi(i=1,2,3,…),使内接正方形与相邻前一个正方形的一边夹角为a,求所有正方形的面积之和.
在边长为a的正方形ABCD中内依次作内接正方形AiBiCiDi(i=1,2,3,…),使内接正方形与相邻前一个正方形的一边夹角为a,求所有正方形的面积之和. 如图所示,在边长为a的正方形组成的网格中,设椭圆C1、C2、C3的离心率分别为e1、e2、e3,则e1、e2、e3的关系为
如图所示,在边长为a的正方形组成的网格中,设椭圆C1、C2、C3的离心率分别为e1、e2、e3,则e1、e2、e3的关系为 (2013•海淀区二模)如图,在边长为a的正方形内有不规则图形Ω.向正方形内随机撒豆子,若撒在图形Ω内和正方形内的豆子数分别为m,n,则图形Ω面积的估计值为( )
(2013•海淀区二模)如图,在边长为a的正方形内有不规则图形Ω.向正方形内随机撒豆子,若撒在图形Ω内和正方形内的豆子数分别为m,n,则图形Ω面积的估计值为( )