题目内容
12．已知等比数列{an}的前n项和为Sn，若a2•a3=2a1，且$\frac{1}{2}{a_4}$与a7的等差中项为$\frac{5}{8}$，则S4=（ ）| A． | 32 | B． | 31 | C． | 30 | D． | 29 |
分析 设等比数列{an}的公比为q，由a2•a3=2a1，且$\frac{1}{2}{a_4}$与a7的等差中项为$\frac{5}{8}$，可得${a}_{1}^{2}{q}^{3}$=2a1，$2×\frac{5}{8}$=$\frac{1}{2}{a_4}$+a7，即5=$2{a}_{1}{q}^{3}$+4${a}_{1}{q}^{6}$，解出再利用等比数列的前n项和公式即可得出．
解答 解：设等比数列{an}的公比为q，∵a2•a3=2a1，且$\frac{1}{2}{a_4}$与a7的等差中项为$\frac{5}{8}$，
∴${a}_{1}^{2}{q}^{3}$=2a1，$2×\frac{5}{8}$=$\frac{1}{2}{a_4}$+a7，即5=$2{a}_{1}{q}^{3}$+4${a}_{1}{q}^{6}$，
∴5=2（2+4q3），解得q=$\frac{1}{2}$，a1=16，
则S4=$\frac{16（1-\frac{1}{{2}^{4}}）}{1-\frac{1}{2}}$=30，
故选：C．
点评 本题考查了等比数列的通项公式及其前n项和公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
7．△ABC中，tanA，tanB是方程6x2-5x+1=0的两根，则tanC=（ ）
| A． | -1 | B． | 1 | C． | $-\frac{5}{7}$ | D． | $\frac{5}{7}$ |
4．已知集合A={x|y=lgx}，B={x|x2-2x-3＜0}，则A∩B=（ ）
| A． | （-1，0） | B． | （0，3） | C． | （-∞，0）∪（3，+∞） | D． | （-1，3） |
1．
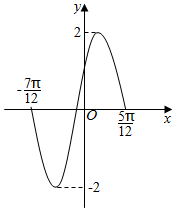已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的部分图象如图所示，则下列判断错误的是（ ）
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的部分图象如图所示，则下列判断错误的是（ ）| A． | A=2 | B． | ω=2 | C． | f（0）=1 | D． | φ=$\frac{5π}{6}$ |
已知椭圆C1：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的离心率为$\frac{{\sqrt{2}}}{2}$，其短轴的下端点在抛物线x2=4y的准线上．