题目内容
(本小题满分14分)
椭圆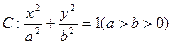 过点P
过点P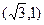 ,且离心率为
,且离心率为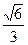 ,F为椭圆的右焦点,
,F为椭圆的右焦点,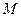 、
、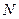 两点在椭圆
两点在椭圆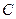 上,且
上,且 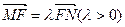 ,定点
,定点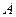 (-4,0).
(-4,0).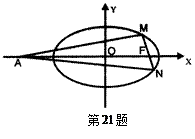
(Ⅰ)求椭圆C的方程;
(Ⅱ)当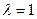 时 ,问:MN与AF是否垂直;并证明你的结论.
时 ,问:MN与AF是否垂直;并证明你的结论.
(Ⅲ)当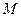 、
、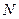 两点在
两点在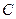 上运动,且
上运动,且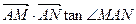 =6
=6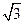 时
时 , 求直线MN的方程.
, 求直线MN的方程.
解:(Ⅰ)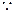 椭圆的离心率为
椭圆的离心率为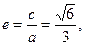
即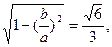 可得
可得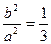
 --2分
--2分
又椭圆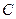 过点P
过点P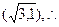
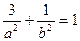
解得 ,
,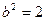 ,椭圆C的方程为
,椭圆C的方程为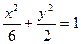 -----
----- -----------4分
-----------4分
(Ⅱ)设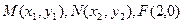 ,
,
则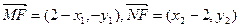 ,
,
当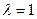 时,
时,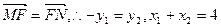 , -----------5分
, -----------5分
由M,N两点在椭圆上,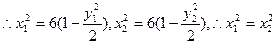 ---------6分
---------6分
若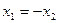 ,则
,则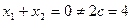 (舍去),
(舍去),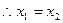 ------------7分
------------7分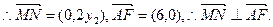 . ------------8分
. ------------8分
(Ⅲ)因为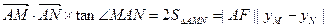 =6
=6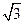 .--9分
.--9分
由已知点F(2,0), 所以|AF|="6, " 即得|yM-yN|=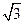
 ------------10分
------------10分
当MN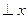 轴时,
轴时,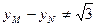 故直线的斜率存在. ------------11分
故直线的斜率存在. ------------11分
不妨设直线MN的方程为: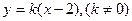 -----
-----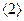
联立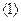 、
、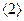 得
得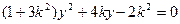
 ------------12分
------------12分 |
|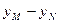 |=
|=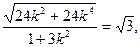 解得
解得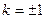 ------------14分
------------14分
此时,直线MN的方程为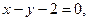 或
或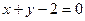 ------------15分
------------15分
解析

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
在极坐标系中,直线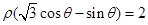 与圆
与圆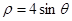 的交点的极坐标为( )
的交点的极坐标为( )
A.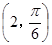 | B.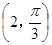 | C.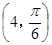 | D.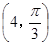 |
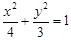 的左、右焦点分别为
的左、右焦点分别为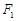 、
、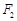 ,直线
,直线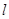 经过点
经过点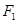 与椭圆交于
与椭圆交于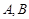 两点。
两点。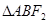 的周长;
的周长;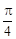 ,求
,求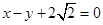 的距离为3。
的距离为3。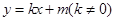 与椭圆相交于不同的两点M,N,当|AM|=|AN|时,求m的取值范围.
与椭圆相交于不同的两点M,N,当|AM|=|AN|时,求m的取值范围.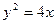 ,过点
,过点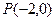 的直线AB交抛物线于点
的直线AB交抛物线于点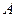 、
、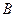 ,若线段
,若线段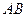 的垂直平分线交
的垂直平分线交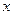 轴于点
轴于点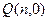 ,求
,求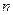 的取值范围.
的取值范围.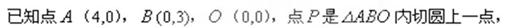
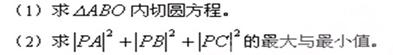
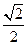 ,且
,且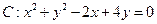 的圆心C。
的圆心C。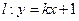 与椭圆交于A、B两点,点
与椭圆交于A、B两点,点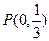 且|PA|=|PB|,求直线
且|PA|=|PB|,求直线 的方程。
的方程。 是一个半椭圆面(如图所示),要保证车辆正常通行,车顶离隧道顶部至少要有
是一个半椭圆面(如图所示),要保证车辆正常通行,车顶离隧道顶部至少要有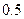 米的距离,现有一货车,车宽
米的距离,现有一货车,车宽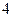 米,车高
米,车高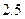 米.
米.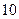 米,则应如何设计隧道才能保证此货车正常通行?
米,则应如何设计隧道才能保证此货车正常通行?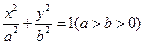 的面积公式.并问,当隧道为双向通行(车道间的距离忽略不记)时,要使此货车安全通过,应如何设计隧道,才会使同等隧道长度下开凿的土方量最小?
的面积公式.并问,当隧道为双向通行(车道间的距离忽略不记)时,要使此货车安全通过,应如何设计隧道,才会使同等隧道长度下开凿的土方量最小?
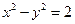
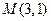 为中点的弦所在的直线的方程
为中点的弦所在的直线的方程 的弦的中点的轨迹方程
的弦的中点的轨迹方程