题目内容
用“五点作图法”在已给坐标系中画出函数y=2sin(
x-
)一个周期内的简图,并指出该函数图象是由函数y=sinx的图象进行怎样的变换而得到的?
| 1 |
| 3 |
| π |
| 6 |
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:根据五点做出函数的简图,再根据y=Asin(ωx+φ)的图象变换规律,得出结论.
解答:
解:列表为
画出图形,如图:
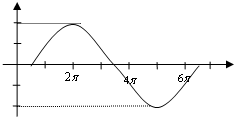 .
.
把y=sinx的图象向右平移
个单位长度,得到y=sin(x-
)的图象;
再把后者所有点的横坐标伸长到原来的3倍(纵坐标不变),得到y=sin(
x-
)的图象;
再把所得图象上所有点的纵坐标伸长到原来的2倍(横坐标不变)
而得到函数y=2sin(
x-
)的图象.
|
0 |
|
π |
|
2π | ||||||||
| x |
|
2π |
|
5π |
| ||||||||
| y | 0 | 2 | 0 | -2 | 0 |
 .
.把y=sinx的图象向右平移
| π |
| 6 |
| π |
| 6 |
再把后者所有点的横坐标伸长到原来的3倍(纵坐标不变),得到y=sin(
| 1 |
| 3 |
| π |
| 6 |
再把所得图象上所有点的纵坐标伸长到原来的2倍(横坐标不变)
而得到函数y=2sin(
| 1 |
| 3 |
| π |
| 6 |
点评:本题考查三点共线的充要条件以及三角函数的图象的变换,主要考查学生对基本结论的理解以及绘制函数图象的能力,属于中档题.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
定义在R上的函数y=f(x)是减函数,且函数y=f(x-2)的图象关于点(2,0)成中心对称,若m,n满足不等式f(m2-2m)+f(2n-n2)≤0.则当1≤m≤4时,
的取值范围是( )
| n |
| m |
A、[-
| ||
B、[-
| ||
C、[-
| ||
D、[-
|
 如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,
如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,