题目内容
(本小题满分12分)在 中,角A,B,C所对的边分别为a,b,c,且
中,角A,B,C所对的边分别为a,b,c,且 .
.
(1)求b;
(2)若 的面积为
的面积为 ,求c.
,求c.
(1) ;(2)
;(2) .
.
【解析】
试题分析:本题主要考查正弦定理、余弦定理、特殊角的三角函数值、三角形面积公式等基础知识,同时考查考生的分析问题解决问题的能力和运算求解能力. 第一问,利用正弦定理将边换成角,消去 ,解出角C,再利用
,解出角C,再利用 解出边b的长;第二问,利用三角形面积公式
解出边b的长;第二问,利用三角形面积公式 ,可直接解出a边的值,再利用余弦定理
,可直接解出a边的值,再利用余弦定理 解出边c的长.
解出边c的长.
试题解析:(Ⅰ)由正弦定理得 ,
,
又 ,所以
,所以 ,
, .
.
因为 ,所以
,所以 . 6分
. 6分
(Ⅱ)因为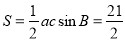 ,
, ,所以
,所以 .
.
据余弦定理可得 ,所以
,所以 . 12分
. 12分
考点:正弦定理、余弦定理、特殊角的三角函数值、三角形面积公式.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
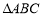 的内角
的内角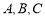 的对边分别为
的对边分别为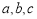 ,
,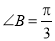 .
. 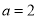 ,
,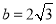 ,求
,求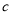 的值;
的值;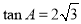 ,求
,求 的值.
的值. ,过C点的圆的切线与AB的延长线交于E点.
,过C点的圆的切线与AB的延长线交于E点.
 ;
; ,
, ,
, ,求AB的长.
,求AB的长. 中,
中, ,则
,则 ( )
( )
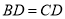 ,过C点的圆的切线与AB的延长线交于E点.
,过C点的圆的切线与AB的延长线交于E点.
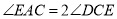 ;
; ,
,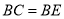 ,
, ,求AB的长.
,求AB的长.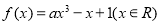 ,若对于任意
,若对于任意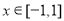 都有
都有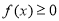 ,则实数a的取值范围为( )
,则实数a的取值范围为( )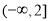 B.
B.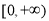 C.
C.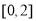 D.
D.
 是等比数列
是等比数列 的前n项和,若
的前n项和,若 ,则
,则 ( )
( ) C.
C. D.1或2
D.1或2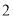 的等腰梯形,则该几何体的体积为( )
的等腰梯形,则该几何体的体积为( )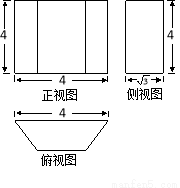
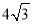 B.
B.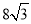 C.
C.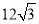 D.
D.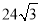
 与双曲线
与双曲线 有共同的焦点
有共同的焦点 和
和 ,且满足
,且满足 是
是 与
与 的等比中项,
的等比中项, 是
是 与
与 的等差中项,则椭圆的离心率为( )
的等差中项,则椭圆的离心率为( ) B.
B. C.
C. D.
D.