题目内容
(本小题满分10分)选修4-1:几何证明选讲
如图,四边形ABDC内接于圆,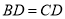 ,过C点的圆的切线与AB的延长线交于E点.
,过C点的圆的切线与AB的延长线交于E点.

(1)求证: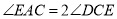 ;
;
(2)若 ,
,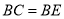 ,
, ,求AB的长.
,求AB的长.
(1)证明详见解析;(2) .
.
【解析】
试题分析:本题主要考查圆内接四边形中的边角关系、切割线定理等基础知识,同时考查考生的读图能力、推理论证能力、运算求解能力. 第一问,由于CE是圆的切线,所以∠ECD=∠CBD,而BD=CD,所以∠BCD=∠CBD,从而∠ECD=∠BCD,所以可得到结论;第二问,因为BD⊥AB,所以AC⊥CD,可得AC=AB,所以得知AC=EC,利用切割线定理得EC2=AEBE,再转化可解出AB的长.
试题解析:(Ⅰ)证明:因为BD=CD,所以∠BCD=∠CBD.
因为CE是圆的切线,所以∠ECD=∠CBD.
所以∠ECD=∠BCD,所以∠BCE=2∠ECD.
因为∠EAC=∠BCE,所以∠EAC=2∠ECD. 5分
(Ⅱ)【解析】
因为BD⊥AB,所以AC⊥CD,AC=AB.
因为BC=BE,所以∠BEC=∠BCE=∠EAC,所以AC=EC.
由切割线定理得EC2=AEBE,即AB2=AE( AE-AB),即
AB2+2 AB-4=0,解得 . 10分
. 10分
考点:圆内接四边形中的边角关系、切割线定理

练习册系列答案
相关题目
 是等差数列,其前n项和为Sn,若
是等差数列,其前n项和为Sn,若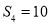 ,
,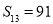 .
.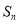 ;
; ,当
,当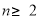 时,
时,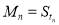 -
-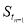 ,其中数列
,其中数列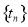 单调递增,且
单调递增,且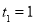 ,
,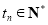 .
.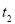 ,
,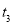 ,使得
,使得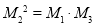 ;
;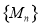 中的各数均为一个整数的平方.
中的各数均为一个整数的平方. ,
, , ,
, , ,则抽取的
,则抽取的 人中,编号在区间
人中,编号在区间 内的人数是 .
内的人数是 .
 B.
B. C.1 D.
C.1 D.
 ”是“方程
”是“方程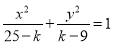 表示双曲线”的( )
表示双曲线”的( ) 中,角A,B,C所对的边分别为a,b,c,且
中,角A,B,C所对的边分别为a,b,c,且 .
. ,求c.
,求c. 、
、 、
、 三种不同型号的轿车,产量之比依次为
三种不同型号的轿车,产量之比依次为 ,为了检验该公司的产品质量,用分层抽样的方法抽取一个容量为
,为了检验该公司的产品质量,用分层抽样的方法抽取一个容量为 的样本,样本中
的样本,样本中 .
.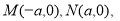 其中
其中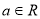 ,若直线
,若直线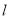 上有且只有一点
上有且只有一点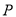 ,使得
,使得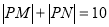 ,则称直线
,则称直线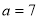 时,坐标平面内不存在黄金直线;
时,坐标平面内不存在黄金直线;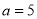 时,坐标平面内有无数条黄金直线;
时,坐标平面内有无数条黄金直线;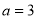 时,黄金点的轨迹是个椭圆;
时,黄金点的轨迹是个椭圆;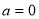 时,坐标平面内有且只有一条黄金直线;
时,坐标平面内有且只有一条黄金直线;