题目内容
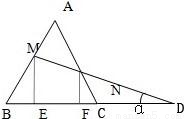
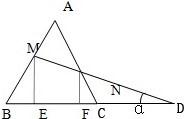 (如图)CD是BC的延长线,AB=BC=CA=CD=a,DM与AB,AC分别交于M点和N点,且∠BDM=α.
(如图)CD是BC的延长线,AB=BC=CA=CD=a,DM与AB,AC分别交于M点和N点,且∠BDM=α.求证:BM=
| 4atanα | ||
|
| 4atanα | ||
|
分析:由题意及图形作ME⊥DC于E,由△ABC是等边三角形,在直角△MBE中利用正切的定义即可;同理,过N作NF⊥BC于F,在直角△NFC中也可求得CN.
解答:证明:证作ME⊥DC于E,由△ABC是等边三角形,在直角△MBE中,
BE=
BM,ME=
BM,
∴tanα=
=
,∴BM=
.
类似地,过N作NF⊥BC于F,在直角△NFC中,可证:CN=
BE=
| 1 |
| 2 |
| ||
| 2 |
∴tanα=
| ME |
| ED |
| ||||
2a-
|
| 4atanα | ||
|
类似地,过N作NF⊥BC于F,在直角△NFC中,可证:CN=
| 4atanα | ||
|
点评:此题考查了学生的识图能力,还考查了解三角形及正切函数定义,还考查了学生的计算能力.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 选修4-1:几何证明选讲
选修4-1:几何证明选讲 如图,AB是半圆的直径,C是AB延长线上一点,CD切半圆于点D,CD=2,DE⊥AB,垂足为E,且E是OB的中点,求BC的长.
如图,AB是半圆的直径,C是AB延长线上一点,CD切半圆于点D,CD=2,DE⊥AB,垂足为E,且E是OB的中点,求BC的长. 选修4-1:几何证明选讲
选修4-1:几何证明选讲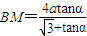 .,
.,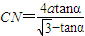 .
.