Question

如图，AB是半圆的直径，C是AB延长线上一点，CD切半圆于点D，CD=2，DE⊥AB，垂足为E，且E是OB的中点，求BC的长．

Answer 1

分析：连接OD，则OD⊥DC，在Rt_△OED中，OE=

1

2

OB=

1

2

OD，所以∠ODE=30°．在Rt_△0DC中，∠DCO=30°，由DC=2，能求出BC的长．

解答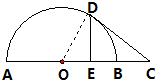：解：连接OD，则OD⊥DC
在Rt△OED中，∵E是OB的中点，
∴OE=

1

2

OB=

1

2

OD
所以∠ODE=30°…（3分）
在Rt△ODC中，∠DCO=30°…（6分）
∵DC=2，
∴OD=DCtan300=

2

3

3

，
∴OC=

22+( 2 3 3 )2

=

4 3

3

所以BC=OC-OB
=OC-OD
=

4 3

3

-

2 3

3

=

2 3

3

．…（10分）

点评：本题考查弦切角的性质和应用，是基础题．解题时要认真审题，仔细解答．