题目内容
设向量

 ,函数
,函数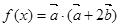 .
.
(1)求函数 的单调递增区间;
的单调递增区间;
(2)求使不等式 成立的
成立的 的取值集合.
的取值集合.
(1)
 ;(2)
;(2) .
.
解析试题分析:(1)本题用向量给出条件,因此首先我们把 求出来,利用向量的数量积运算,可得
求出来,利用向量的数量积运算,可得 ,然后我们三角函数化为
,然后我们三角函数化为 的形式,再利用正弦函数的性质解题,在变形过程中,注意使
的形式,再利用正弦函数的性质解题,在变形过程中,注意使 .在
.在 都大于0的情况下,
都大于0的情况下,
 的单调增区间只要解不等式
的单调增区间只要解不等式 即得.(2)不等式
即得.(2)不等式 是一个三角不等式,因
是一个三角不等式,因 ,同样只要利用余弦函数的性质即可.
,同样只要利用余弦函数的性质即可.
试题解析:(1) 


 . 5′
. 5′
由 ,得
,得
 ,
,
∴ 的单调递增区间为
的单调递增区间为
 . 8′
. 8′
(2) 由 ,得
,得 .
.
由 ,得
,得 ,则
,则 ,
,
即
 . ∴使不等式
. ∴使不等式 成立的
成立的 的取值集合为
的取值集合为 . 14′
. 14′
考点:(1)向量的数量积与三角函数的单调性;(2)复合函数的导数与余弦函数的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (
( ,c是实数常数)的图像上的一个最高点
,c是实数常数)的图像上的一个最高点 ,与该最高点最近的一个最低点是
,与该最高点最近的一个最低点是 ,
, 的解析式及其单调增区间;
的解析式及其单调增区间; ,且
,且 ,角A的取值范围是区间M,当
,角A的取值范围是区间M,当 时,试求函数
时,试求函数 .
. 的值;
的值; 的值.
的值. +
+ )cos(
)cos( ,α∈(-
,α∈(- ,0),求α的值;
,0),求α的值; ,x∈(
,x∈( 中,角
中,角 、
、 、
、 所对的边分别为
所对的边分别为 、
、 、
、 ,且
,且 .
. 的值;
的值; ,
, ,求
,求 中,角A、B、C的对边分别为a、b、c,且角A、B、C成等差教列.
中,角A、B、C的对边分别为a、b、c,且角A、B、C成等差教列. ,求边c的值;
,求边c的值; ,求角A的最大值.
,求角A的最大值. 的顶点在原点,始边与
的顶点在原点,始边与 轴的正半轴重合,终边经过点
轴的正半轴重合,终边经过点 .
. 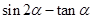 的值;
的值; ,求函数
,求函数 在区间
在区间 上的取值范围.
上的取值范围.  ,且其图象的相邻对称轴间的距离为
,且其图象的相邻对称轴间的距离为 .
. 在区间
在区间 上的值域;
上的值域; 中,若
中,若
 求
求 ,函数
,函数 .
. 的最小正周期;
的最小正周期; 分别为
分别为 内角
内角 、
、 、
、 的对边, 其中
的对边, 其中 且
且 ,求
,求 和
和 .
.