题目内容
已知函数
，且其图象的相邻对称轴间的距离为
.
（I）求
在区间
上的值域；
（II）在锐角
中，若
求的面积.
(I) 
的值域是
；（II）
．
解析试题分析：(I) 求在区间上的值域，解这类问题常常通过三角恒等变形，把它转化为一个角的一个三角函数来解，本题通过三角恒等变形得
，因为其图象的相邻对称轴间的距离为，故它的周期
，可得
，这样得
，从而可求值域；（II）在锐角中，若由(I)可得
,求的面积，只需求出
的值即可，又因为可用余弦定理
，求得
，从而有
求得面积．
试题解析：（I）
2分
3分
由条件知，，又
，
. 4分
， 
， 
，
的值域是. 7分
（II）由
，得, 9分
由
及余弦定理，得， 12分
的面积
. 14分
考点：三角恒等变化，三角函数值域，解三角形．
练习册系列答案
相关题目
中,已知
.
; 
求角A的大小.
，函数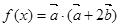
.
的单调递增区间；
成立的
的取值集合．
与
，其中
，求
和
的值；
，求
的值域.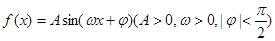
的图象的一部分如下图所示.
的解析式；
时，求函数
的最大值与最小值及相应的
的值．
，
.
的值；
、
，
，
，求
的值.
.
的最小正周期；
上的函数值的取值范围.
）（ω＞0，0＜
＝
，且a∈（0，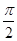
），求f（a）的值．