题目内容
在某校篮球队的首轮选拔测试中,参加测试的五名同学的投篮命中率分别为 ,
, ,
, ,
, ,
, ,每人均有10次投篮机会,至少投中六次才能晋级下一轮测试,假设每人每次投篮相互独立,则晋级下一轮的人数大约为
,每人均有10次投篮机会,至少投中六次才能晋级下一轮测试,假设每人每次投篮相互独立,则晋级下一轮的人数大约为
- A.2人
- B.3人
- C.4人
- D.5人
B
分析:根据题意,由概率的意义,计算可得五名同学在10次中每人投中的可能次数,比较可得其中投中次数大于等于6次的人数,即可得答案.
解答:根据题意,五名同学每人均有10次投篮机会,其篮命中率分别为 ,
, ,
, ,
, ,
, ,
,
则10次中每人投中的次数依次为6,5, ,7.5,
,7.5, ;
;
其中投中的次数大于等于6次的有3人,
则晋级下一轮的人数大约为3;
故选B.
点评:本题考查概率的定义及其应用,关键是正确理解概率的意义.
分析:根据题意,由概率的意义,计算可得五名同学在10次中每人投中的可能次数,比较可得其中投中次数大于等于6次的人数,即可得答案.
解答:根据题意,五名同学每人均有10次投篮机会,其篮命中率分别为
 ,
, ,
, ,
, ,
, ,
,则10次中每人投中的次数依次为6,5,
 ,7.5,
,7.5, ;
;其中投中的次数大于等于6次的有3人,
则晋级下一轮的人数大约为3;
故选B.
点评:本题考查概率的定义及其应用,关键是正确理解概率的意义.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
 沿一个正方体三个面的对角线截得的几何体如图所示,则该几何体的左视图为
沿一个正方体三个面的对角线截得的几何体如图所示,则该几何体的左视图为



 在
在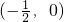 内恒有y>0,那么a的取值范围是
内恒有y>0,那么a的取值范围是