题目内容
17.已知x,y满足不等式组$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≥0}\\{2x-y-5≤0}\end{array}\right.$,求(1)z=x+2y的最大值;
(2)z=x2+y2-10y+25的最小值.
分析 (1)作出不等式组对应的平面区域,利用直线平行进行求解即可.
(2)z的几何意义是两点间的距离的平方,利用点到直线的距离公式进行求解即可.
解答 解:(1)由约束条件$\left\{\begin{array}{l}{x-y+2≥0}\\{x+y-4≥0}\\{2x-y-5≤0}\end{array}\right.$表示的可行域如下图所示,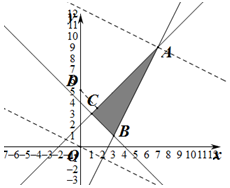
由z=x+2y,得y=-$\frac{1}{2}x+\frac{z}{2}$,
平移直线y=-$\frac{1}{2}x+\frac{z}{2}$,由图象可知当直线y=-$\frac{1}{2}x+\frac{z}{2}$经过点A时,直线y=-$\frac{1}{2}x+\frac{z}{2}$的截距最大,此时z最大,
由$\left\{\begin{array}{l}{x-y+2=0}\\{2x-y-5=0}\end{array}\right.$得$\left\{\begin{array}{l}{x=7}\\{y=9}\end{array}\right.$,即A(7,9),此时z=7+2×9=25;
(2)z=x2+y2-10y+25=x2+(y-5)2,z的几何意义为点P(x,y)到点(0,5)的距离的平方;
由图知,最小值为(0,5)到直线x-y+2=0的距离的平方,
即d2=($\frac{|0-5+2|}{\sqrt{2}}$)2=$\frac{9}{2}$.经检验,垂足在线段AC上.
点评 本题主要考查线性规划的应用,可以直线平移以及两点间的距离公式是解决本题的关键.

练习册系列答案
相关题目
7.7人排成一排,甲、乙两人必须相邻,且甲、乙都不与丙相邻,则不同的排法有( )种.
| A. | 960种 | B. | 840种 | C. | 720种 | D. | 600种 |
2.椭圆$\frac{x^2}{{{{10}^{\;}}}}+\frac{y^2}{{{m^{\;}}}}=1$的焦距为6,则m的值为( )
| A. | m=1 | B. | m=19 | C. | m=1 或 m=19 | D. | m=4或m=16 |