题目内容
在一次抽奖活动中,假设某10张券中有一等奖1张,可获价值200元的奖品;有二等奖2张,每张可获价值100元的奖品;有三等奖3张,每张可获价值50元的奖品;其余4张没有奖,某顾客从此10张券中任抽2张,求:(1)该顾客中奖的概率;
(2)该顾客获得的奖品总价值X(元)的分布列和期望.
【答案】分析:(1)先求中奖的对立事件“没中奖”的概率,求“没中奖”的概率是古典概型,再用对立事件减法公式或得答案.
(2)ξ的所有可能值为:0,50,100,150,200,250,300,用古典概型分别求概率,列出分布列,再求期望即可.
解答:解:(Ⅰ)设某顾客从此10张券中任抽2张中奖的事件为A
则某顾客从此10张券中任抽2张没有中奖的概率
P(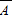 )=
)= =
=
P(A)=1-P(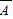 )=1-
)=1- =
=
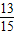 ,
,
即该顾客中奖的概率为 .
.
(Ⅱ)ξ的所有可能值为:0,50,100,150,200,250,300(元).
且P(ξ=0)=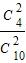 =
=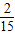 =
=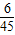 ,
,
P(ξ=50)=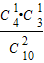 =
=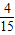 =
=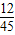 ,
,
P(ξ=100)=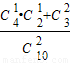 =
= ,
,
P(ξ=150)=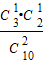 =
= =
=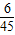 ,
,
P(ξ=200)= =
= =
=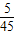
P(ξ=250)=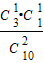 =
=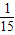 =
=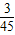
P(ξ=300)=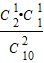 =
=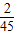
故ξ有分布列:
从而期望Eξ=0×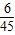 +50×
+50×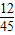 +100×
+100×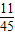 +150×
+150×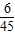 +200×
+200× +250×
+250×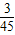 +300×
+300×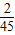 =110
=110
点评:本题考查古典概型、排列组合、离散型随机变量的分布列和期望,及利用概率知识解决问题的能力.
(2)ξ的所有可能值为:0,50,100,150,200,250,300,用古典概型分别求概率,列出分布列,再求期望即可.
解答:解:(Ⅰ)设某顾客从此10张券中任抽2张中奖的事件为A
则某顾客从此10张券中任抽2张没有中奖的概率
P(
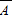 )=
)= =
=
P(A)=1-P(
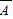 )=1-
)=1- =
=
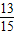 ,
,即该顾客中奖的概率为
 .
.(Ⅱ)ξ的所有可能值为:0,50,100,150,200,250,300(元).
且P(ξ=0)=
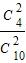 =
=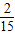 =
=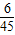 ,
,P(ξ=50)=
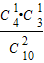 =
=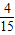 =
=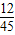 ,
,P(ξ=100)=
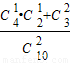 =
= ,
,P(ξ=150)=
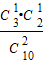 =
= =
=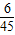 ,
,P(ξ=200)=
 =
= =
=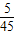
P(ξ=250)=
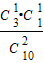 =
=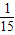 =
=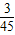
P(ξ=300)=
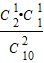 =
=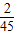
故ξ有分布列:
| ξ | 50 | 100 | 150 | 200 | 250 | 300 | |
| P | 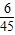 | 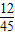 |  |  |  |  | 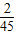 |
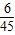 +50×
+50×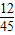 +100×
+100×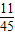 +150×
+150×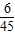 +200×
+200× +250×
+250×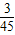 +300×
+300×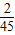 =110
=110点评:本题考查古典概型、排列组合、离散型随机变量的分布列和期望,及利用概率知识解决问题的能力.

练习册系列答案
相关题目