题目内容
5.己知向量$\overrightarrow{s}$=($\sqrt{3}$sin2x-1,cosx),$\overrightarrow{t}$=($\frac{1}{2}$,cosx),设f(x)=$\overrightarrow{s}$$•\overrightarrow{t}$+1.(1)求函数f(x)的最小正周期及在区间[0,$\frac{π}{2}$]上的最大值;
(2)已知在△ABC中,内角A,B,C的对边分别为a,b,c,其中A,B为锐角,f(A+$\frac{π}{6}$)=$\frac{8}{5}$,f($\frac{B}{2}$$-\frac{π}{12}$)-1=$\frac{\sqrt{10}}{10}$,又a+b=$\sqrt{2}$+1,求a,b,c的值.
分析 (1)利用向量的数量积的坐标运算与三角函数中的恒等变换应用可求得f(x)=sin(2x+$\frac{π}{6}$)+$\frac{1}{2}$,从而可求函数f(x)的最小正周期及在[0,$\frac{π}{2}$]上的最大值.
(2)由f(A+$\frac{π}{6}$)=$\frac{8}{5}$,化简解得cosA,sinA的值,由f($\frac{B}{2}$$-\frac{π}{12}$)-1=$\frac{\sqrt{10}}{10}$,可求sinB,cosB的值,利用两角和的余弦函数公式可求cosC,sinC的值,由正弦定理可得a+b=2R(sinA+sinB)=2R($\frac{\sqrt{5}}{5}$+$\frac{\sqrt{10}}{10}$)=$\sqrt{2}$+1,解得2R的值,利用正弦定理即可依次解得a,b,c的值.
解答 解:(1)∵f(x)=$\overrightarrow{s}$$•\overrightarrow{t}$+1.
=$\frac{\sqrt{3}}{2}$sin2x-$\frac{1}{2}$+$\frac{1+cos2x}{2}$+1
=$\frac{\sqrt{3}}{2}$sin2x+$\frac{1}{2}$cos2x+1
=sin(2x+$\frac{π}{6}$)+1,
∴f(x)的最小正周期T=$\frac{2π}{2}$=π;
∵x∈[0,$\frac{π}{2}$],
∴2x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{7π}{6}$],
∴sin(2x+$\frac{π}{6}$)∈[-$\frac{1}{2}$,1],sin(2x+$\frac{π}{6}$)+1∈[$\frac{1}{2}$,2],
∴f(x)=sin(2x+$\frac{π}{6}$)+1的最大值为:2.
(2)∵A,B为锐角,
∴由f(A+$\frac{π}{6}$)=sin[2(A+$\frac{π}{6}$)+$\frac{π}{6}$]+1=sin(2A+$\frac{π}{2}$)+1=$\frac{8}{5}$,可得:cos2A=$\frac{3}{5}$=2cos2A-1,
解得:cosA=$\frac{2\sqrt{5}}{5}$,sinA=$\frac{\sqrt{5}}{5}$,
由f($\frac{B}{2}$$-\frac{π}{12}$)-1=sin[2($\frac{B}{2}$$-\frac{π}{12}$)+$\frac{π}{6}$]+1-1=sinB=$\frac{\sqrt{10}}{10}$,cosB=$\frac{3\sqrt{10}}{10}$,
∴cosC=-cos(A+B)=sinAsinB-cosAcosB=-$\frac{\sqrt{2}}{2}$,结合C∈(0,π),可得:C=$\frac{3π}{4}$,
∴由正弦定理可得:$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2R$,
∴a+b=2R(sinA+sinB)=2R($\frac{\sqrt{5}}{5}$+$\frac{\sqrt{10}}{10}$)=$\sqrt{2}$+1,解得:2R=$\sqrt{10}$,
∴a=2RsinA=$\sqrt{10}$×$\frac{\sqrt{5}}{5}$=$\sqrt{2}$,b=2RsinB=$\sqrt{10}$×$\frac{\sqrt{10}}{10}$=1,c=2RsinC=$\sqrt{10}$×$\frac{\sqrt{2}}{2}$=$\sqrt{5}$.
点评 本题考查向量的数量积的坐标运算与三角函数中的恒等变换应用,考查角函数的周期性与单调性,考查运算求解的能力,属于中档题.

| A. | -3 | B. | 3 | C. | 1 | D. | -1 |
| A. | ?x0∈R,使log2x0≤0成立 | B. | ?x0∈R,使log2x>0成立 | ||
| C. | ?x∈R,都有log2x≥0成立 | D. | ?x∈R,都有log2x>0成立 |
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | t | 4 | 4.5 |
| A. | 4.5 | B. | 3.5 | C. | 3.15 | D. | 3 |
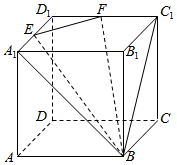 如图,已知正方体ABCD-A1B1C1D1的边长为2,点E,F分别是A1D1,C1D1的中点.
如图,已知正方体ABCD-A1B1C1D1的边长为2,点E,F分别是A1D1,C1D1的中点.