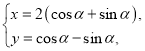题目内容
【题目】已知数列![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() ),与数列
),与数列![]() :
:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() ),记
),记![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)求![]() 的表达式;
的表达式;
(3)已知![]() ,且存在正整数
,且存在正整数![]() ,使得在
,使得在![]() 中有4项为100,求
中有4项为100,求![]() 的值,并指出哪4项为100.
的值,并指出哪4项为100.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为100.
为100.
【解析】
(1)直接求得![]() 关于
关于![]() 的表达式再求解即可.
的表达式再求解即可.
(2)先求得![]() ,再猜测
,再猜测![]() 的表达式利用数学归纳法求证即可.
的表达式利用数学归纳法求证即可.
(3)分别写出![]() 的值,判断这12项的中的4项和为100,再求出
的值,判断这12项的中的4项和为100,再求出![]() 的值即可求出哪4项和为100.
的值即可求出哪4项和为100.
(1)易得![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() …
…
故![]() ,解得
,解得![]() .
.
(2)由![]() 得
得
![]() .
.
猜测![]() ,用数学归纳法证明,
,用数学归纳法证明,
①当![]() 时,
时, ![]() 成立.
成立.
②假设当![]() ,
,![]() 时等式成立,即
时等式成立,即![]() ,则当
,则当![]() 时,
时,
![]()
![]()
![]() 也成立.
也成立.
根据①,②可以判定:当![]() 时,
时, ![]()
(3)根据(2)有![]() .
.
当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() ;
;
当![]() 时,
时, ![]() ;
;
因为![]() 是奇数,
是奇数,![]() ,
,![]() ,
,![]() 均为负数.故这些数均不可能取到100,
均为负数.故这些数均不可能取到100,
故当![]() 或
或![]() ,即
,即![]() ,
,![]() 时
时![]() ,
,![]() ,
,![]() ,
,![]() 为100.
为100.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目