题目内容
【题目】已知动圆![]() 在圆
在圆![]() :
:![]() 外部且与圆
外部且与圆![]() 相切,同时还在圆
相切,同时还在圆![]() :
:![]() 内部与圆
内部与圆![]() 相切.
相切.
(1)求动圆圆心![]() 的轨迹方程;
的轨迹方程;
(2)记(1)中求出的轨迹为![]() ,
,![]() 与
与![]() 轴的两个交点分别为
轴的两个交点分别为![]() 、
、![]() ,
,![]() 是
是![]() 上异于
上异于![]() 、
、![]() 的动点,又直线
的动点,又直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 、
、![]() 分别交直线
分别交直线![]() 于
于![]() 、
、![]() 两点,求证:
两点,求证:![]() 为定值.
为定值.
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)由直线与圆相切,则![]() ,则
,则![]() 点的轨迹是以
点的轨迹是以![]() ,
,![]() 为焦点的椭圆,即可求得椭圆方程;
为焦点的椭圆,即可求得椭圆方程;
(2)方法一:设![]() ,分别求得直线
,分别求得直线![]() 的方程,直线
的方程,直线![]() 的方程,分别求得点
的方程,分别求得点![]() 和
和![]() 的坐标,则
的坐标,则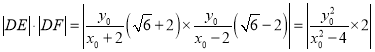 ,即可求得
,即可求得![]() 为定值;
为定值;
方法二:设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,联立直线
,联立直线![]() 的方程与直线
的方程与直线![]() 的方程,求出点
的方程,求出点![]() 坐标,将点
坐标,将点![]() 坐标代入椭圆方程,即可求得
坐标代入椭圆方程,即可求得![]() ,
,![]() 为定值.
为定值.
(1)设动圆![]() 的半径为
的半径为![]() ,由已知得
,由已知得![]() ,
,![]() ,
,![]() ,
,
![]()
![]() 点的轨迹是以
点的轨迹是以![]() ,
,![]() 为焦点的椭圆,
为焦点的椭圆,
设椭圆方程:![]() (
(![]() ),则
),则![]() ,
,![]() ,则
,则![]() ,
,
方程为:![]() ;
;
(2)解法一:设![]() ,由已知得
,由已知得![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
直线![]() 的方程为:
的方程为:![]() ,
,
直线![]() 的方程为:
的方程为:![]() ,
,
当![]() 时,
时,![]() ,
,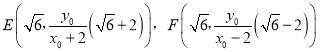 ,
,
![]()
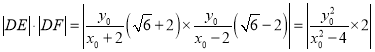 ,
,
又![]()
![]() 满足
满足![]() ,
,
![]()
![]() ,
,
![]()
![]() 为定值.
为定值.
解法二:由已知得![]() ,
,![]() ,设直线
,设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,由已知得,
,由已知得,![]() ,
,![]() 存在且不为零,
存在且不为零,
![]() 直线
直线![]() 的方程为:
的方程为:![]() ,
,
直线![]() 的方程为:
的方程为:![]() ,
,
当![]() 时,
时,![]() ,
,![]() ,
,
![]()
![]() ,
,
联立直线![]() 和直线
和直线![]() 的方程,可得
的方程,可得![]() 点坐标为
点坐标为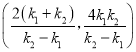 ,
,
将![]() 点坐标代入椭圆方程
点坐标代入椭圆方程![]() 中,得
中,得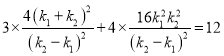 ,
,
即![]() ,
,
整理得![]() ,
,
![]()
![]() ,
,![]()
![]() ,
,
![]()
![]() 为定值.
为定值.

练习册系列答案
相关题目