题目内容
已知函数f(x)=2lnx+x2,若f(x2-1)≤1,则实数x的取值范围是 .
考点:对数的运算性质
专题:函数的性质及应用
分析:由f(x)=2lnx+x2,x>0,利用导数性质求出f(x)是增函数,f(t)=2lnt+t2,t=x2-1,由f(t)≤1,得0<t≤1,所以0<x2-1≤1,由此能求出实数x的取值范围.
解答:
解:∵f(x)=2lnx+x2,
∴x>0,f′(x)=2x+
=2•
>0,
∴f(x)是增函数,
f(t)=2lnt+t2,t=x2-1,
令2lnt+t2=1,t=1,
∴f(t)≤1,∵f(t)是增函数,
∴0<t≤1,
∴0<x2-1≤1,∴1<x2≤2,
解得-
≤x<-1或1<x≤
.
∴实数x的取值范围是[-
,-1)∪(1,
].
故答案为:[-
,-1)∪(1,
].
∴x>0,f′(x)=2x+
| 2 |
| x |
| x2+1 |
| x |
∴f(x)是增函数,
f(t)=2lnt+t2,t=x2-1,
令2lnt+t2=1,t=1,
∴f(t)≤1,∵f(t)是增函数,
∴0<t≤1,
∴0<x2-1≤1,∴1<x2≤2,
解得-
| 2 |
| 2 |
∴实数x的取值范围是[-
| 2 |
| 2 |
故答案为:[-
| 2 |
| 2 |
点评:本题考查实数的取值范围的求法,解题时要认真审题,导数性质的灵活运用.

练习册系列答案
相关题目
“m=3”是“椭圆
+
=1的离心率e=
”的( )
| x2 |
| 5 |
| y2 |
| m |
| ||
| 5 |
| A、充分但不必要条件 |
| B、必要但不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知2x+y=2,且x,y都为正实数,则xy+
的最小值为( )
| 1 |
| xy |
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
若平面向量
,
满足
+
=(1,5),
-
=(2,3),则
•
=( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、13 | ||
B、
| ||
C、
| ||
| D、26 |
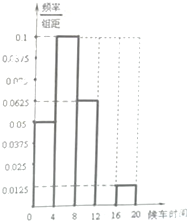 常州公交公司为了调整302线路发车的时间间隔,在某站点对乘客进行了候车时间的调查,以下是候车时间的频率分布表和频率分布直方图.
常州公交公司为了调整302线路发车的时间间隔,在某站点对乘客进行了候车时间的调查,以下是候车时间的频率分布表和频率分布直方图.