题目内容
5. 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上一点与它的左、右两个焦点F1,F2的距离之和为2$\sqrt{2}$,且它的离心率与双曲线x2-y2=2的离心率互为倒数.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上一点与它的左、右两个焦点F1,F2的距离之和为2$\sqrt{2}$,且它的离心率与双曲线x2-y2=2的离心率互为倒数.(1)求椭圆的方程;
(2)如图,点A为椭圆上一动点(非长轴端点),AF1的延长线与椭圆交于点B,AO的延长线与椭圆交于点C.
①当直线AB的斜率存在时,求证:直线AB与BC的斜率之积为定值;
②求△ABC面积的最大值,并求此时直线AB的方程.
分析 (1)易知2a=2$\sqrt{2}$,e=$\frac{\sqrt{2}}{2}$,从而解得;
(2)①设A(xA,yA),B(xB,yB),则C(-xA,-yA),从而设直线BA的方程为y=k(x+1),联立方程化简(2k2+1)x2+4k2x+2k2-2=0,从而可得xA+xB=-$\frac{4{k}^{2}}{2{k}^{2}+1}$,yA+yB=k$\frac{2}{2{k}^{2}+1}$,从而证明.
②分情况讨论以分别确定△ABC的面积的取值范围,从而解得.
解答 解:(1)由椭圆的定义知2a=2$\sqrt{2}$,
双曲线x2-y2=2的离心率为$\sqrt{2}$,
故椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的离心率e=$\frac{\sqrt{2}}{2}$,
故a=$\sqrt{2}$,c=1,b=1;
故椭圆的方程为$\frac{{x}^{2}}{2}$+y2=1;
(2)①证明:设A(xA,yA),B(xB,yB),则C(-xA,-yA),
设直线BA的方程为y=k(x+1),
联立方程$\left\{\begin{array}{l}{y=k(x+1)}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$化简得,
(2k2+1)x2+4k2x+2k2-2=0,
∴xA+xB=-$\frac{4{k}^{2}}{2{k}^{2}+1}$,
yA+yB=k(xA+xB)+2k=k(-$\frac{4{k}^{2}}{2{k}^{2}+1}$+2)=k$\frac{2}{2{k}^{2}+1}$,
∴kABkBC=k•$\frac{{y}_{B}+{y}_{A}}{{x}_{B}+{x}_{A}}$=$\frac{2{k}^{2}}{-4{k}^{2}}$=-$\frac{1}{2}$;
②当直线AB的斜率不存在时,
可知A(-1,$\frac{\sqrt{2}}{2}$),B(-1,-$\frac{\sqrt{2}}{2}$),C(1,-$\frac{\sqrt{2}}{2}$),
故S△ABC=$\sqrt{2}$,
当直线AB的斜率存在时,由①知,
xA+xB=-$\frac{4{k}^{2}}{2{k}^{2}+1}$,xAxB=$\frac{2{k}^{2}-2}{2{k}^{2}+1}$,
故|xA-xB|=$\sqrt{({x}_{A}+{x}_{B})^{2}-4{x}_{A}{x}_{B}}$
=$2\sqrt{2}$•$\frac{\sqrt{{k}^{2}+1}}{2{k}^{2}+1}$,
故|AB|=$\sqrt{1+{k}^{2}}$|xA-xB|
=$2\sqrt{2}$•$\sqrt{1+{k}^{2}}$•$\frac{\sqrt{{k}^{2}+1}}{2{k}^{2}+1}$,
点C到直线AB的距离d=$\frac{|k(-{x}_{A}+1)+{y}_{A}|}{\sqrt{{k}^{2}+1}}$=$\frac{2|k|}{\sqrt{{k}^{2}+1}}$,
故S△ABC=$\frac{1}{2}$•($2\sqrt{2}$•$\sqrt{1+{k}^{2}}$•$\frac{\sqrt{{k}^{2}+1}}{2{k}^{2}+1}$)•$\frac{2|k|}{\sqrt{{k}^{2}+1}}$
=2$\sqrt{2}$$\sqrt{\frac{{k}^{2}({k}^{2}+1)}{(2{k}^{2}+1)^{2}}}$
=2$\sqrt{2}$•$\sqrt{\frac{1}{4}-\frac{1}{4(2{k}^{2}+1)^{2}}}$<$\sqrt{2}$,
故△ABC面积的最大值为$\sqrt{2}$,此时AB的方程为x+1=0.
点评 本题考查了椭圆与双曲线的性质应用,同时考查了数形结合的思想应用及分类讨论的思想应用,关键在于化简运算.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案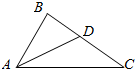 如图,在△ABC中,∠B=$\frac{π}{2}$,∠BAC的平分线交BC于点D,AD=$\sqrt{2}$,AC=$\sqrt{6}$,则△ABC的面积为$\frac{3\sqrt{3}}{4}$.
如图,在△ABC中,∠B=$\frac{π}{2}$,∠BAC的平分线交BC于点D,AD=$\sqrt{2}$,AC=$\sqrt{6}$,则△ABC的面积为$\frac{3\sqrt{3}}{4}$. 在平面直角坐标系xOy中,对于⊙O:x2+y2=1来说,P是坐标系内任意一点,点P到⊙O的距离SP的定义如下:若P与O重合,SP=r;若P不与O重合,射线OP与⊙O的交点为A,SP=AP的长度(如图).
在平面直角坐标系xOy中,对于⊙O:x2+y2=1来说,P是坐标系内任意一点,点P到⊙O的距离SP的定义如下:若P与O重合,SP=r;若P不与O重合,射线OP与⊙O的交点为A,SP=AP的长度(如图).