题目内容
已知矩形ABCD，P为ABCD外一点，PA⊥面ABCD，G为△PAC的重心，则
(
+
+
)=
．
| 1 |
| 3 |
| AB |
| AD |
| AP |
| AG |
| AG |
分析：利用向量的加法法则，结合三角形重心的概念，即可得到结论．
解答：解：由题意，
(
+
+
)=
(
+
)
∵G为△PAC的重心
∴
=
×
×(
+
)=
(
+
)
∴
(
+
+
)=
故答案为：
| 1 |
| 3 |
| AB |
| AD |
| AP |
| 1 |
| 3 |
| AC |
| AP |
∵G为△PAC的重心
∴
| AG |
| 2 |
| 3 |
| 1 |
| 2 |
| AC |
| AP |
| 1 |
| 3 |
| AC |
| AP |
∴
| 1 |
| 3 |
| AB |
| AD |
| AP |
| AG |
故答案为：
| AG |
点评：本题考查向量在几何中的应用，解题的关键是正确运用向量的加法法则，属于中档题．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
如图，已知矩形ABCD所在平面外一点P，PA⊥平面ABCD，E、F分别是AB、PC的中点．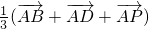
=________．
= ．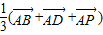