题目内容
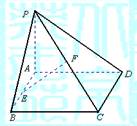
 如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点.
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E、F分别是AB、PC的中点.(1)求证:EF∥平面PAD;
(2)若∠PDA=45°,求EF与平面ABCD所成的角的大小.
分析:(1)取PD中点G,连接AG、FG,利用三角形中位线定理,我们易判断四边形AEFG是平行四边形,AG∥EF,进而结合线面平行的判定定理,我们易得到EF∥平面PAD;
(2)过G作GH⊥AD,垂足为H,则可得∠GAH为AG与平面ABCD所成的角,即为所求角.
(2)过G作GH⊥AD,垂足为H,则可得∠GAH为AG与平面ABCD所成的角,即为所求角.
解答: (1)证明:取PD中点G,连接AG、FG,
(1)证明:取PD中点G,连接AG、FG,
因为EF分别为AB、PC的中点,
所以AE=
AB,GF∥DC且GF=
DC,
又在矩形ABCD中AB∥CD且AB=CD,
所以AE∥GF且AE=GF,
所以四边形AEFG是平行四边形,
所以AG∥EF且AG=EF
又AG?平面PAD,EF?平面PAD.
所以EF∥平面PAD;
(2)解:∵AG∥EF,
∴AG与平面ABCD所成的角等于EF与平面ABCD所成的角
过G作GH⊥AD,垂足为H,则GH∥PA
∵PA⊥平面ABCD,∴GH⊥平面ABCD,
∴∠GAH为AG与平面ABCD所成的角,即为所求角,
∵∠PDA=45°,G为PD的中点
∴∠GAH=45°
即EF与平面ABCD所成的角为45°.
 (1)证明:取PD中点G,连接AG、FG,
(1)证明:取PD中点G,连接AG、FG,因为EF分别为AB、PC的中点,
所以AE=
| 1 |
| 2 |
| 1 |
| 2 |
又在矩形ABCD中AB∥CD且AB=CD,
所以AE∥GF且AE=GF,
所以四边形AEFG是平行四边形,
所以AG∥EF且AG=EF
又AG?平面PAD,EF?平面PAD.
所以EF∥平面PAD;
(2)解:∵AG∥EF,
∴AG与平面ABCD所成的角等于EF与平面ABCD所成的角
过G作GH⊥AD,垂足为H,则GH∥PA
∵PA⊥平面ABCD,∴GH⊥平面ABCD,
∴∠GAH为AG与平面ABCD所成的角,即为所求角,
∵∠PDA=45°,G为PD的中点
∴∠GAH=45°
即EF与平面ABCD所成的角为45°.
点评:本题考查的知识点是直线与平面平行的判定,考查线面角,熟练掌握判定定理内容、正确找出线面角是关键

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目


 BC,FO
BC,FO


 为矩阵
为矩阵 属于λ的一个特征向量,求实数a,λ的值及A2。
属于λ的一个特征向量,求实数a,λ的值及A2。 (α为参数),曲线D的参数方程为
(α为参数),曲线D的参数方程为 ,(t为参数)。若曲线C、D有公共点,求实数m的取值范围。
,(t为参数)。若曲线C、D有公共点,求实数m的取值范围。
 计20分。请在答题卡指定区域作答。解答应写出文字
计20分。请在答题卡指定区域作答。解答应写出文字 说明、证明过程或演算
说明、证明过程或演算 步骤。
步骤。
 为矩阵
为矩阵 属于λ的一个特征向量,求实数a,λ的值及A2。
属于λ的一个特征向量,求实数a,λ的值及A2。 在平面直角坐标系xoy中,曲线C的参数方程为
在平面直角坐标系xoy中,曲线C的参数方程为 (α为参数),曲线D的参数方程为
(α为参数),曲线D的参数方程为 ,(t为参数)。若曲线C、D有公共点,求实数m的取值范围。
,(t为参数)。若曲线C、D有公共点,求实数m的取值范围。 正实数,且ab=2。求证:(1+2a)(1+b)≥9。
正实数,且ab=2。求证:(1+2a)(1+b)≥9。