题目内容
10.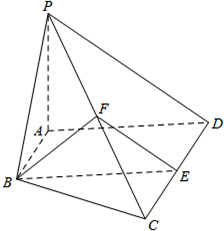 如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AD=CD=2AB=2PA=4,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD和PC的中点.
如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AD=CD=2AB=2PA=4,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD和PC的中点.(1)求证:PA⊥底面ABCD;
(2)求△BEF的面积.
分析 (1)根据条件,利用平面和平面垂直的性质定理可得PA⊥平面ABCD.
(2)求出EF,BE,sin∠FEB,即可求出△BEF的面积.
解答 (1)证明:∵PA⊥AD,平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴由平面和平面垂直的性质定理可得PA⊥平面ABCD.
(2)解:由题意,PD=$\sqrt{{2}^{2}+{4}^{2}}$=2$\sqrt{5}$,BE=4,
∴EF=$\sqrt{5}$
∵BE∥AD,EF∥PD,
∴∠FEB=∠PDA,
∴sin∠FEB=$\frac{2}{2\sqrt{5}}$=$\frac{1}{\sqrt{5}}$,
∴△BEF的面积为$\frac{1}{2}×4×\sqrt{5}×\frac{1}{\sqrt{5}}$=2.
点评 本题主要考查直线和平面垂直的判定定理,考查△BEF的面积的计算,属于中档题.

练习册系列答案
相关题目