题目内容

18．求下列函数的导数
（1）y=xeex
（2）y=$\frac{{x}^{3}-1}{sinx}$
（3）y=2e-x
（4）y=2xsin（2x+5）

分析 根据导数的运算法则求导即可．

解答 解：（1）y′=（xeex）′=（xe）′ex+xe（ex）′=exe-1ex+xeex，
（2）y′=（$\frac{{x}^{3}-1}{sinx}$）′=$\frac{（{x}^{3}-1）′sinx-（{x}^{3}-1）（sinx）′}{si{n}^{2}x}$=$\frac{3{x}^{2}sinx-（{x}^{3}-1）cosx}{si{n}^{2}x}$，
（3）y′=（2e-x）′=-2e-x，
（4）y′=（2xsin（2x+5））′=2sin（2x+5）-4xcos（2x+5）

点评 本题考查了导数的运算法则，属于基础题．

练习册系列答案
相关题目
2．已知双曲线C中心在原点，焦点在x轴上，点P（-2，0）与其渐近线的距离为$\frac{\sqrt{10}}{5}$，过点P作斜率为$\frac{1}{6}$的直线交双曲线于A、B两点，点A、P、B在x轴上的射影分别是A1、P1、B1，且|P1O|是|P1A1|与|P1B1|的等比中项，求双曲线的离心率．
9．已知函数f（x）=lnx+ax+$\frac{1+a}{x}$（a＞-$\frac{1}{2}$），（其中e=2.718…）．
（1）讨论f（x）的单调性及极值点个数；
（2）若f（x）在[1，e}]的最小值为f（1），求实数a的取值范围．
6．${A}_{2n}^{11-n}{+A}_{n+4}^{2n}$=80640．
13．在△ABC中，若a2=3bcsinA，则$\frac{b}{c}$+$\frac{c}{b}$的最大值为$\sqrt{13}$．
3．已知t为常数，且0＜t＜1，函数g（x）=$\frac{1}{2}$（x+$\frac{1-t}{x}$）（x＞0）最小值和函数h（x）=$\sqrt{{x}^{2}-2x+2+t}$的最小值都是函数f（x）=-x3+ax2+bx（a，b∈R）的零点．
（1）用含a的式子表示b，并求出a的取值范围；
（2）求函数f（x）在区间[1，2]上的最大值和最小值．
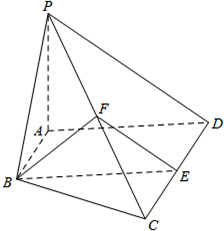10．如图，在四棱锥P-ABCD中，AB∥CD，AB⊥AD，AD=CD=2AB=2PA=4，平面PAD⊥底面ABCD，PA⊥AD，E和F分别是CD和PC的中点．
（1）求证：PA⊥底面ABCD；
（2）求△BEF的面积．
7．已知△ABC的面积是S，且$\overrightarrow{AB}•\overrightarrow{AC}$=$\sqrt{2}$S．
（1）求sinA的值；
（2）若|$\overrightarrow{AB}$|=3，|$\overrightarrow{AB}-\overrightarrow{AC}$|=2$\sqrt{3}$，求sinB的值．
8．已知等比数列{an}的前n项和为Sn，且S3=2，S6-S3=4，则S9-S6=（　　）
A．8B．4C．2D．1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网