题目内容
20.若$\frac{1}{cosθ}$-$\frac{1}{sinθ}$=1,求sin2θ的值.分析 已知等式左边通分并利用同分母分式的减法法则计算,整理后两边平方,利用完全平方公式及同角三角函数间的基本关系化简,求出sinθcosθ的值,原式利用二倍角的正弦函数公式化简,将sinθcosθ的值代入计算即可求出值.
解答 解:$\frac{1}{cosθ}$-$\frac{1}{sinθ}$=$\frac{sinθ-cosθ}{sinθcosθ}$=1,即sinθ-cosθ=sinθcosθ,
两边平方得:(sinθ-cosθ)2=1-2sinθcosθ=sin2θcos2θ,
解得:sinθcosθ=-1+$\sqrt{2}$或sinθcosθ=-1-$\sqrt{2}$,
则sin2θ=2sinθcosθ=-2±2$\sqrt{2}$.
点评 此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
8.已知等比数列{an}的前n项和为Sn,且S3=2,S6-S3=4,则S9-S6=( )
| A. | 8 | B. | 4 | C. | 2 | D. | 1 |
10.已知复数z=1+i,则$\frac{2}{z}$-1=( )
| A. | -i | B. | 1 | C. | i | D. | -1 |
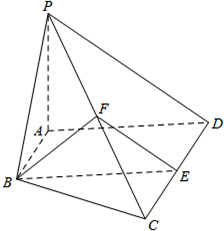 如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AD=CD=2AB=2PA=4,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD和PC的中点.
如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AD=CD=2AB=2PA=4,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD和PC的中点.