题目内容
15.设m是正整数,试证明等式:${∫}_{-π}^{π}$sinmxdx=0.分析 求出被积函数的原函数,分别代入积分上限和积分下限后作差得答案.
解答 证明::${∫}_{-π}^{π}$sinmxdx=$-\frac{1}{m}cosmx{|}_{-π}^{π}$=$-\frac{1}{m}cosmπ$$-[-\frac{1}{m}cos(-mπ)]$
=$-\frac{1}{m}cosmπ+\frac{1}{m}cosmπ=0$.
点评 本题考查了定积分,考查了简单的复合函数的求导,是基础题.

练习册系列答案
相关题目
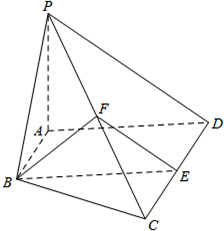 如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AD=CD=2AB=2PA=4,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD和PC的中点.
如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,AD=CD=2AB=2PA=4,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD和PC的中点.