题目内容
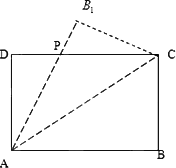
如图所示,设矩形ABCD的AB=2,AD=3,E、F分别是AD、BC的三等分点中靠近D、C的那个分点,G为CD边上的一个点.将此矩形沿EF折成直二面角.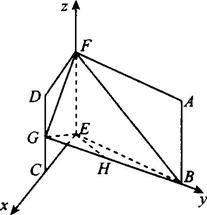
第18题图
(1)当平面BFG⊥平面BEG时,求G点的位置;
(2)在(1)的前提下,求直线GE与平面BFG所成的角.
答案:(1)建立如图所示的坐标系,有F(0,0,2)、E(0,0,0).
设G(1,0,z),则![]() =(1,0,z),
=(1,0,z),![]() =(0,2,0),
=(0,2,0),![]() =(0,-2,2).
=(0,-2,2).

第18题图
又设平面BEG的法向量为m=(a,b,c),则
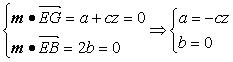 .
.
令c=1,得m=(-z,0,1).
设平面BFG的法向量为n=(p,q,r),则
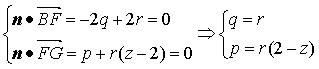 .
.
令r=1,得n=(2-z,1,1).
令m⊥n,得-z(2-z)+1=0![]() z=1.
z=1.
故当且仅当G为CD中点时,平面BFG⊥平面BEF.
(2)作EH⊥BG于H.
∴平面BFG⊥平面BEG,∴EH⊥平面BFG.
于是,∠EGH就是直线GE与平面BFG所成的角.
在ABGE中,∵EH·BG=BE·EG,
∴EH=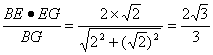
故sin∠EGH=![]() .
.
∴∠EGH=arcsin![]() .
.

练习册系列答案
相关题目
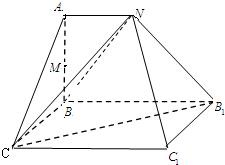 已知某几何体的直观图和三视图如图所示,其正视图为直角梯形,侧视图为等腰直角三角形,俯视图为矩形.
已知某几何体的直观图和三视图如图所示,其正视图为直角梯形,侧视图为等腰直角三角形,俯视图为矩形.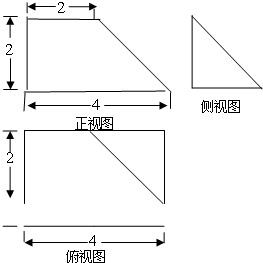
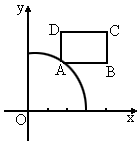
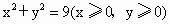 上移动,且AB、AD两边分别平行于x轴、y轴.求矩形ABCD面积的最小值及对应点A的坐标.
上移动,且AB、AD两边分别平行于x轴、y轴.求矩形ABCD面积的最小值及对应点A的坐标.