Question

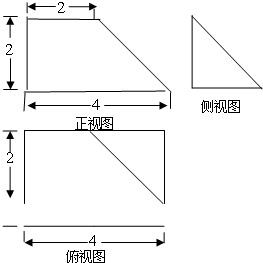
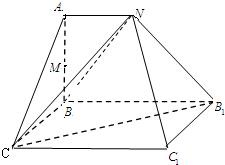已知某几何体的直观图和三视图如图所示，其正视图为直角梯形，侧视图为等腰直角三角形，俯视图为矩形．
（Ⅰ）证明：BN⊥平面B₁C₁N；
（II）求二面角C-NB₁-C₁的余弦值；
（III）设M为线段AB的中点，在线段BC上是否存在一点P，使得MP∥平面CNB₁？若存在，指出点P的位置；若不存在，请说明理由．

Answer 1

分析：法一建立空间直角坐标系，（Ⅰ）求出向量

BN

•

NB1

=0，

BN

•

B1C1

=0即可证明：BN⊥平面B₁C₁N；
（II）求出平面CNB₁和平面NB₁C₁的法向量，利用公式求出其余弦值；
（III）设

MP

=（a，0，-1），利用

MP

⊥

n

?

MP

•

n

=0，求出a可使得MP∥平面CNB₁
法二：几何法，（Ⅰ）由已知得B₁C₁⊥平面BNB₁，可得B₁C₁⊥BN，再求证BN⊥B₁N即可证明结论．
（II）过N作NQ

∥ .

.

B₁C₁，∠CNQ是二面角C-B₁N-Q的平面角，然后求解即可．
（III）延长BA、B₁N交于R，连接CR，利用比例关系，推出P的位置，使得MP∥平面CNB₁

解答：解：解法一：（Ⅰ）证明
∵该几何体的正视图为直角梯形，侧视图为等腰直角三角形，俯视图为矩形，
∴BA，BC，BB₁两两垂直．
以BC，BB₁，BA分别为x，y，z轴建立空间直角坐标系，（1分）

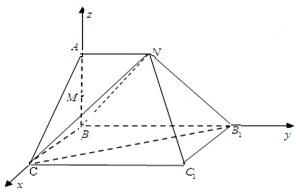
则N（0，2，2），B₁（0，4，0），C₁（2，4，0），C（2，0，0）
∵

BN

•

NB1

=（0，2，2）•（0，2，-2）=4-4=0

BN

•

B1C1

=（0，2，2）•（2，0，0）=0（3分）
∴BN⊥NB₁，BN⊥B₁C₁，又NB₁与B₁C₁相交于B₁，
∴BN⊥平面C₁B₁N；（4分）

（Ⅱ）由（Ⅰ）知，

BN

=（0，2，2）是平面C₁B₁N的一个法向量，（5分）
设

n

=(x，y，z)为平面NCB₁的一个法向量，
则

n • CN =0 n • NB1 =0

?

(x，y，z)•(-2，2，2)=0 (x，y，z)•(0，2，-2)=0

?

-x+y+z=0 y-z=0

，取

n

=（2，1，1），（7分）
∴cos＜

BN

，

n

＞=

BN • n

| BN • n |

=

3

3

，
即二面角C-NB₁-C₁的余弦值为

3

3

．（9分）
（Ⅲ）∵M（0，0，1）．设P（a，0，0）为BC上一点，则

MP

=（a，0，-1），∵MP∥平面CNB₁，
∴

MP

⊥

n

?

MP

•

n

=（a，0，-1）•（2，1，1）=2a-1=0?a=

1

2

．（12分）
又MP?平面CNB₁，∴MP∥平面CNB₁，∴当BP=

1

2

时MP∥平面CNB₁．（13分）
解法二：
（Ⅰ）证明：由已知得B₁C₁⊥平面BNB₁，∴B₁C₁⊥BN，
BN=2

2

=B₁N，BB₁=4，∴BB₁²=BN²+B₁N²，∴BN⊥B₁N
又B₁C₁与B₁N交于B₁，∴BN⊥平面C₁B₁N；
（Ⅱ）过N作NQ

∥ .

.

B₁C₁，则BC∥QN，又BN⊥平面C₁B₁N，
∴CQ⊥平面C₁B₁N，则CQ⊥B₁N，QN⊥B₁N，∴∠CNQ是二面角C-B₁N-Q的平面角θ，
在Rt△CNQ中，NQ=2，CQ=2

2

，∴CN=2

3

，cosθ=

NQ

CN

=

3

3

；

（Ⅲ）延长BA、B₁N交于R，连接CR，∵MP∥平面CNB₁，
MP?平面CBR，平面CBR∩平面CRN于CR，
∴MP∥CR，△RB₁B中AN

∥ .

.

1

2

BB₁，∴A为RB中点，
∴

BP

BC

=

BM

BR

=

1

4

，∴BP=

1

2

，因此存在P点使MP∥平面CNB₁．

点评：本题主要考查直线与直线，直线与平面，平面与平面位置关系等基础知识；考查空间想象能力，推理论证能力和运算求解能力．