题目内容
13.已知为a,b实数,且ab≠0,则下列命题错误的是( )| A. | 若a≠b,则$\frac{a+b}{2}>\sqrt{ab}$ | B. | 若a>0,b>0,则$\frac{a+b}{2}≥\sqrt{ab}$ | ||
| C. | 若$\frac{a+b}{2}≥\sqrt{ab}$,则a>0,b>0 | D. | 若$\frac{a+b}{2}>\sqrt{ab}$,则a≠b |
分析 根据基本不等式的性质分别进行判断即可.
解答 解:A.当a=-1,b=-3时,不等式$\frac{a+b}{2}>\sqrt{ab}$不成立,故A错误,
B.若a>0,b>0,则$\frac{a+b}{2}≥\sqrt{ab}$,成立,故B正确,
C.若$\frac{a+b}{2}≥\sqrt{ab}$,则ab≥0,a+b≥0,
∵ab≠0,∴ab>0,a+b>0,即a>0,b>0,成立,故C正确,
D.若$\frac{a+b}{2}>\sqrt{ab}$,则a,b>0,
且$\frac{a+b}{2}-\sqrt{ab}=\frac{a-2\sqrt{ab}+b}{2}$>0,即$\frac{(\sqrt{a}-\sqrt{b})}{2}$>0,
则$\sqrt{a}≠\sqrt{b}$,即a≠b,
故D正确,
故选:A
点评 本题主要考查命题的真假判断,涉及基本不等式的性质和应用,注意基本不等式成立的条件.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
3.已知函数f(x)=sin(2ωx一$\frac{π}{4}$)(ω>0)的最小正周期为π,则函数f(x)的图象( )
| A. | 关于点($\frac{π}{8}$,0)对称 | B. | 关于直线x=$\frac{π}{8}$对称 | ||
| C. | 关于点(-$\frac{π}{4}$,0)对称 | D. | 关于直线x=-$\frac{π}{4}$对称 |
4.已知集合A={x|x<-2},B={x|x2>4},则“x∈A”是“x∈B”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
1.已知i是虚数单位,若复数z满足z=$\frac{{i}^{3}}{1+i}$,则z为( )
| A. | $\frac{1+i}{2}$ | B. | $\frac{1-i}{2}$ | C. | $\frac{-1-i}{2}$ | D. | $\frac{-1+i}{2}$ |
18.若命题:“?x∈R,x2-2ax+a≤0”为假命题,则$\frac{{2{a^2}+1}}{a}$的最小值是( )
| A. | $2\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $2\sqrt{3}$ | D. | $\sqrt{3}$ |
3.下列不等式中成立的是( )
| A. | sin140°<sin30° | B. | cos140°<cos130° | C. | tan40°<tan30° | D. | sin40°<sin30° |
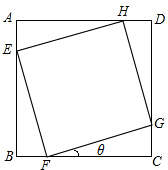 如图所示,某住宅小区内有一正方形草地ABCD,现欲在其中修建一个正方形花坛EFGH,若已知花坛面积为正方形草地面积的$\frac{2}{3}$,则θ=arctan(2-$\sqrt{3}$).
如图所示,某住宅小区内有一正方形草地ABCD,现欲在其中修建一个正方形花坛EFGH,若已知花坛面积为正方形草地面积的$\frac{2}{3}$,则θ=arctan(2-$\sqrt{3}$).