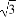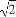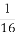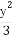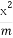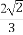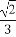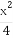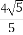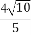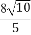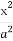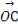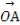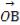题目内容
已知椭圆C: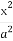 +
+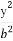 =1(a>b>0)的一个顶点A(2,0),离心率为
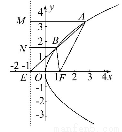
=1(a>b>0)的一个顶点A(2,0),离心率为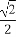 ,直线y=k(x-1)与椭圆C交于不同的两点M,N.
,直线y=k(x-1)与椭圆C交于不同的两点M,N.
(1)求椭圆C的方程.
(2)当△AMN的面积为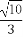 时,求k的值.
时,求k的值.
(1)  +
+ =1 (2) k=±1
=1 (2) k=±1
【解析】(1)a=2,e= =
= ,c=
,c= ,b=
,b= ,
,
椭圆C: +
+ =1.
=1.
(2)设M(x1,y1),N(x2,y2),则由 ,消y得
,消y得
(1+2k2)x2-4k2x+2k2-4=0,
∵直线y=k(x-1)过椭圆内点(1,0),
∴Δ>0恒成立,
由根与系数的关系得
x1+x2= ,x1x2=
,x1x2= ,
,
S△AMN= ×1×|y1-y2|=
×1×|y1-y2|= ×|kx1-kx2|
×|kx1-kx2|
= =
= =
= .
.
即7k4-2k2-5=0,解得k=±1.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目