题目内容
7.已知幂函数f(x)的图象过点(2,$\sqrt{2}$),则关于a的不等式f(a+1)<f(3)的解是{a|-1≤a<2}.分析 设幂函数f(x)=xα,α为常数.把点(2,$\sqrt{2}$)代入可得:$\sqrt{2}={2}^{α}$,解得α,再利用幂函数的单调性即可解出.
解答 解:设幂函数f(x)=xα,α为常数.
由于图象过点(2,$\sqrt{2}$),
代入可得:$\sqrt{2}={2}^{α}$,
解得$α=\frac{1}{2}$.
∴f(x)=$\sqrt{x}$.
可知:函数f(x)在[0,+∞)单调递增,
∵f(a+1)<f(3),
∴0≤a+1<3,
解得-1≤a<2.
∴关于a的不等式f(a+1)<f(3)的解集是{a|-1≤a<2}.
故答案为:{a|-1≤a<2}.
点评 本题考查了幂函数的解析式与单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.如果函数f(x)的定义域为[-1,1],那么函数f(x2-1)的定义域是( )
| A. | [0,2] | B. | [-1,1] | C. | [-2,2] | D. | [-$\sqrt{2}$,$\sqrt{2}$] |
2.下列函数中,既是偶函数又在(0,+∞)上单调递增的是 ( )
| A. | y=x3 | B. | y=-x2 | C. | y=2x | D. | y=ln|x| |
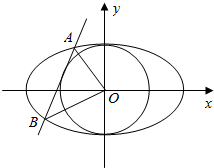 如图,已知圆O:x2+y2=1,直线l:y=kx+b(k>0,b>0)是圆的一条切线,且l与椭圆$\frac{{x}^{2}}{2}$+y2=1交于不同的两点A,B.
如图,已知圆O:x2+y2=1,直线l:y=kx+b(k>0,b>0)是圆的一条切线,且l与椭圆$\frac{{x}^{2}}{2}$+y2=1交于不同的两点A,B.