题目内容
12.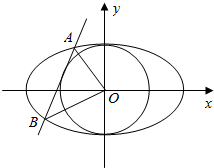 如图,已知圆O:x2+y2=1,直线l:y=kx+b(k>0,b>0)是圆的一条切线,且l与椭圆$\frac{{x}^{2}}{2}$+y2=1交于不同的两点A,B.
如图,已知圆O:x2+y2=1,直线l:y=kx+b(k>0,b>0)是圆的一条切线,且l与椭圆$\frac{{x}^{2}}{2}$+y2=1交于不同的两点A,B. (1)求k与b的关系;
(2)若弦AB的长为$\frac{4}{3}$,求直线l的方程.
分析 (1)直接由圆心到切线的距离等于圆的半径求得k与b的关系;
(2)联立直线方程与圆锥曲线方程,化为关于x的一元二次方程,利用弦长公式求得k的值,进一步得到b的值,则直线l的方程可求.
解答 解:(1)∵直线l:y=kx+b(k>0,b>0)是圆圆O:x2+y2=1的一条切线,
∴$\frac{|b|}{\sqrt{{k}^{2}+1}}=1$,即b2=k2+1 ①;
(2)联立$\left\{\begin{array}{l}{\frac{{x}^{2}}{2}+{y}^{2}=1}\\{y=kx+b}\end{array}\right.$,得(2k2+1)x2+4kbx+2b2-2=0.
设A(x1,y1),B(x2,y2),则${x}_{1}+{x}_{2}=-\frac{4kb}{2{k}^{2}+1},{x}_{1}{x}_{2}=\frac{2{b}^{2}-2}{2{k}^{2}+1}$,
∴|AB|=$\sqrt{1+{k}^{2}}\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{1+{k}^{2}}\sqrt{(-\frac{4kb}{2{k}^{2}+1})^{2}-4\frac{2{b}^{2}-2}{2{k}^{2}+1}}=\frac{4}{3}$ ②,
联立①②解得:k=1或k=-1(舍).
则b=$\sqrt{{k}^{2}+1}=\sqrt{2}$.
∴直线l的方程为y=x+$\sqrt{2}$.
点评 本题考查圆锥曲线和直线的位置关系,考查了弦长公式的应用,涉及直线与圆锥曲线的关系问题,常采用联立直线与圆锥曲线方程,运用一元二次方程的根与系数的关系求解,属中档题.

练习册系列答案
 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
2.下列命题中的假命题是( )
| A. | ?x0∈R,lgx0=0 | B. | ?x0∈R,tanx0=0 | C. | ?x∈R,x3>0 | D. | ?x∈R,2x>0 |
3.已知不同直线a,b,l,不同平面α,β,γ,则下列命题正确的是( )
| A. | 若a⊥l,b⊥l,则a∥b | B. | 若α⊥γ,β⊥γ,则α∥β | C. | 若β⊥γ,b⊥γ,则b∥β | D. | 若α⊥l,β⊥l,则α∥β |
4.在椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上取三点,其横坐标满足x1+x3=2x2,三点与某一焦点的连线段长分别为r1,r2,r3.则r1,r2,r3满足( )
| A. | r1,r2,r3成等差数列 | B. | $\frac{1}{{r}_{1}}$+$\frac{1}{{r}_{2}}$=$\frac{2}{{r}_{3}}$ | ||
| C. | r1,r2,r3成等比数列 | D. | 以上结论全不对 |
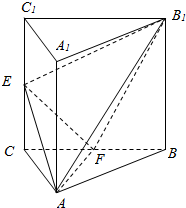 如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1=2,E,F分别是CC1,BC的中点.
如图,三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1=2,E,F分别是CC1,BC的中点.