题目内容
((本小题满分12分)
中心在原点,焦点在x轴上的椭圆,率心率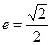 ,此椭圆与直线
,此椭圆与直线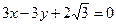 交于A、B两点,且OA⊥OB(其中O为坐标原点).
交于A、B两点,且OA⊥OB(其中O为坐标原点).
(1)求椭圆方程;
(2)若M是椭圆上任意一点,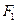 、
、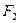 为椭圆的两个焦点,求
为椭圆的两个焦点,求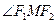 的取值范围;
的取值范围;
中心在原点,焦点在x轴上的椭圆,率心率
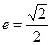 ,此椭圆与直线
,此椭圆与直线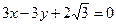 交于A、B两点,且OA⊥OB(其中O为坐标原点).
交于A、B两点,且OA⊥OB(其中O为坐标原点).(1)求椭圆方程;
(2)若M是椭圆上任意一点,
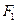 、
、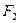 为椭圆的两个焦点,求
为椭圆的两个焦点,求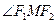 的取值范围;
的取值范围;(1)
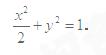
(2)
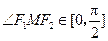
(1)设椭圆方程为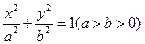 .
.
∵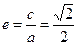 ,
,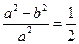 ,
,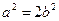 .
.
∴ 椭圆方程化简为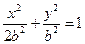 .
.
∵ 椭圆与直线相交,
椭圆与直线相交,
解方程组: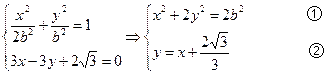
由①代入②,代简得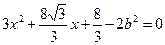 .
.
根据韦达定理,设A(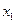 ,
,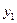 ),B(
),B(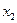 ,
,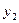 ),
),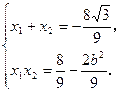
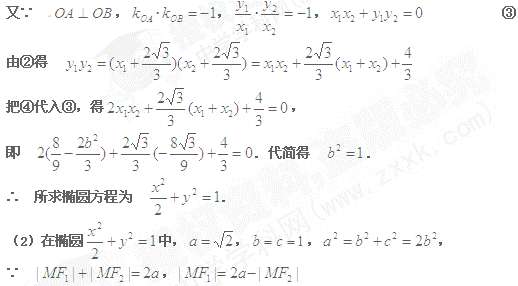
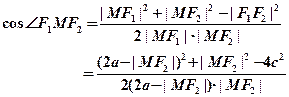
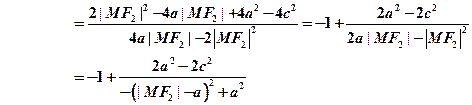
其中: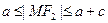 .
.
当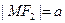 时,cos
时,cos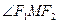 有最小值为0,
有最小值为0, 此时,
此时,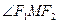 有最大值为
有最大值为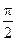 ,当
,当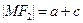 时,
时,
即M点与椭圆长轴左端点重合,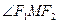 有最小值为0,故
有最小值为0,故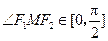 .
.
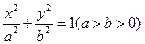 .
.∵
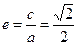 ,
,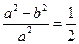 ,
,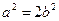 .
.∴ 椭圆方程化简为
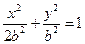 .
.∵
 椭圆与直线相交,
椭圆与直线相交,解方程组:
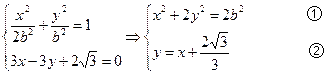
由①代入②,代简得
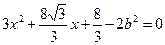 .
.根据韦达定理,设A(
 ,
, ),B(
),B(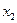 ,
,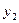 ),
),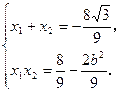
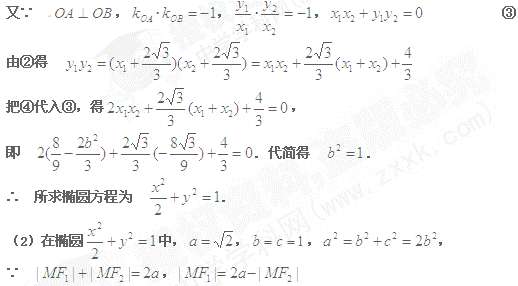
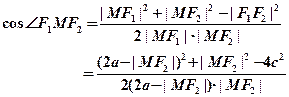
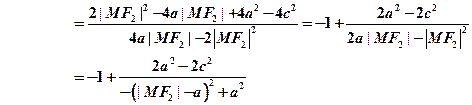
其中:
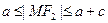 .
. 当
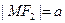 时,cos
时,cos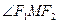 有最小值为0,
有最小值为0, 此时,
此时,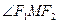 有最大值为
有最大值为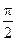 ,当
,当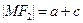 时,
时,即M点与椭圆长轴左端点重合,
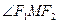 有最小值为0,故
有最小值为0,故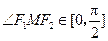 .
.
练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
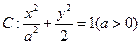 的左右焦点分别为
的左右焦点分别为 、
、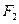 ,
,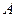 是椭圆
是椭圆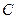 上的一点,且
上的一点,且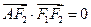 ,坐标原点
,坐标原点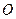 到
到 直线
直线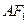 的距离为
的距离为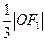 .
.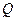 是椭圆
是椭圆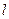 交
交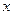 轴于点
轴于点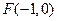 ,交
,交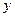 轴于点
轴于点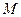 ,若
,若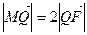 ,求直线
,求直线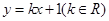 与椭圆
与椭圆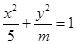 恒有公共点,则实数
恒有公共点,则实数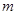 的取值范围为( )
的取值范围为( )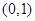
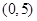
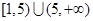
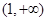
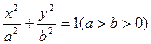 的两个焦点
的两个焦点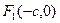 、
、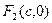 ,M是椭圆上一点,且满足
,M是椭圆上一点,且满足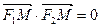 .
.  的取值范围;
的取值范围; 到椭圆上的点的最远距离为
到椭圆上的点的最远距离为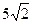 ;
;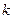 (
(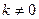 )的直线
)的直线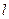 与椭圆G相交于不同的两点A、B,Q为AB的中点,问:A、B两点能否关于过点
与椭圆G相交于不同的两点A、B,Q为AB的中点,问:A、B两点能否关于过点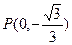 、Q的直线对称?若能,求出
、Q的直线对称?若能,求出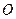 ,长轴长为
,长轴长为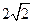 ,离心率
,离心率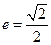 ,过右焦点
,过右焦点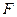 的直线
的直线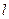 交椭圆于
交椭圆于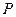 ,
,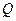 两点.
两点.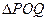 的面积;
的面积;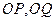 为邻边的平行四边形是矩形,求满足该条件的直线
为邻边的平行四边形是矩形,求满足该条件的直线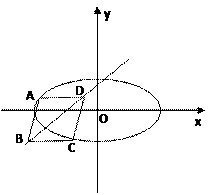
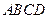 的顶点
的顶点 在椭圆
在椭圆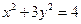 上,对角线
上,对角线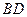 所在直线的斜率为1.
所在直线的斜率为1.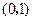 时,求直线
时,求直线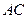
 的方程;
的方程;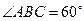 时,求菱形
时,求菱形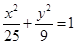 上一点M到焦点
上一点M到焦点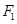 的距离为2,
的距离为2,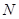 是
是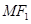 的中点,
的中点,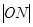 等于( *** )
等于( *** )
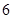
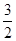
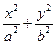 (a>b>0)的离心率
(a>b>0)的离心率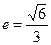 ,过点
,过点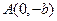 和
和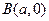 的直线与原点的距离为
的直线与原点的距离为
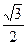 .
.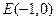 ,若直线
,若直线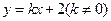 与椭圆交于
与椭圆交于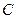 、
、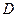 两点.问:是否存在
两点.问:是否存在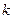 的值,使以
的值,使以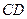 为直径的圆过
为直径的圆过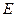 点?请说明理由.
点?请说明理由.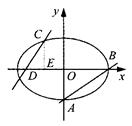
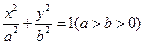 的左、右顶点,椭圆的长轴长为4,且点
的左、右顶点,椭圆的长轴长为4,且点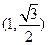 在该椭圆上。
在该椭圆上。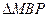 为锐角三角形
为锐角三角形