题目内容
设椭圆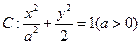 的左右焦点分别为
的左右焦点分别为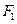 、
、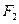 ,
,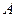 是椭圆
是椭圆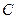 上的一点,且
上的一点,且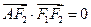 ,坐标原点
,坐标原点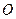 到
到 直线
直线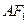 的距离为
的距离为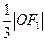 .
.
(1)求椭圆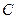 的方程;
的方程;
(2) 设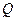 是椭圆
是椭圆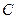 上的一点,过点
上的一点,过点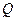 的直线
的直线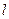 交
交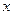 轴于点
轴于点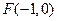 ,交
,交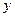 轴于点
轴于点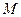 ,若
,若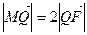 ,求直线
,求直线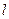 的斜率.
的斜率.
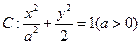 的左右焦点分别为
的左右焦点分别为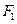 、
、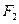 ,
,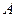 是椭圆
是椭圆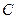 上的一点,且
上的一点,且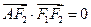 ,坐标原点
,坐标原点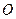 到
到 直线
直线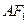 的距离为
的距离为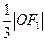 .
.(1)求椭圆
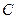 的方程;
的方程;(2) 设
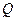 是椭圆
是椭圆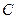 上的一点,过点
上的一点,过点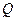 的直线
的直线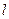 交
交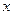 轴于点
轴于点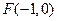 ,交
,交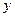 轴于点
轴于点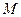 ,若
,若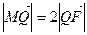 ,求直线
,求直线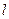 的斜率.
的斜率.解: (Ⅰ)由题设知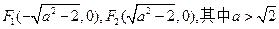
由于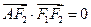 ,则有
,则有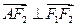 , A
, A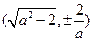 ……..2分
……..2分
故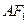 所在直线方程为
所在直线方程为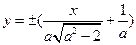 …………3分
…………3分
所以坐标原点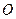 到直线
到直线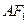 的距离为
的距离为 ,
,
又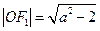 ,所以
,所以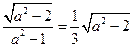 ,解得:
,解得: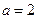 .…….5分
.…….5分
所求椭圆的方程为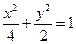 .…………6分
.…………6分
(2)由题意可知直线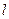 的斜率存在,设直线斜率为
的斜率存在,设直线斜率为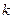 ,则直线
,则直线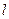 的方程为
的方程为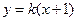 ,
,
则有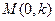 .……7分
.……7分
设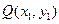 ,由于
,由于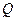 、
、
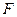 、
、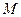 三点共线,且
三点共线,且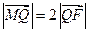 .
.
根据题意得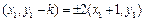 ,解得
,解得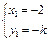 或
或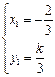 .……10分
.……10分
又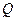 在椭圆
在椭圆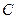 上,故
上,故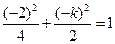 或
或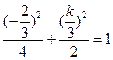 ,解得
,解得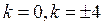 ,
,
综上,直线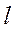 的斜率为
的斜率为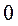 或
或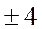 …………12分
…………12分
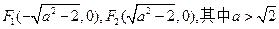
由于
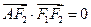 ,则有
,则有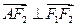 , A
, A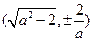 ……..2分
……..2分故
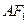 所在直线方程为
所在直线方程为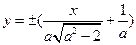 …………3分
…………3分所以坐标原点
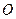 到直线
到直线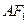 的距离为
的距离为 ,
,又
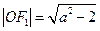 ,所以
,所以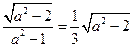 ,解得:
,解得: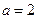 .…….5分
.…….5分所求椭圆的方程为
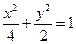 .…………6分
.…………6分(2)由题意可知直线
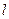 的斜率存在,设直线斜率为
的斜率存在,设直线斜率为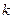 ,则直线
,则直线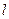 的方程为
的方程为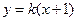 ,
,则有
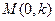 .……7分
.……7分设
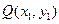 ,由于
,由于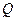 、
、
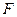 、
、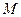 三点共线,且
三点共线,且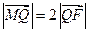 .
.根据题意得
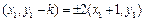 ,解得
,解得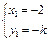 或
或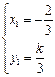 .……10分
.……10分 又
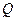 在椭圆
在椭圆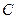 上,故
上,故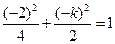 或
或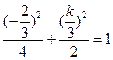 ,解得
,解得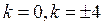 ,
, 综上,直线
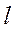 的斜率为
的斜率为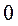 或
或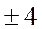 …………12分
…………12分略

练习册系列答案
相关题目
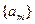 是首项为
是首项为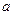 ,公差为
,公差为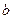 的等差数列,
的等差数列,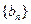 是首项为
是首项为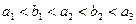 ,其中
,其中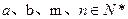 .
.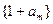 与数列
与数列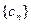 ,求数列
,求数列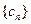 的通项公式;
的通项公式;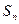 ,求证:
,求证: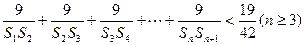 .
.
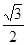
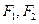 分别是椭圆
分别是椭圆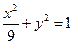 的左右焦点.
的左右焦点.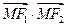 的最大值和最小值;
的最大值和最小值;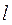 与椭圆交于不同的两点A、B,且
与椭圆交于不同的两点A、B,且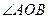
 为钝角,(其中O为坐标原点),求直线
为钝角,(其中O为坐标原点),求直线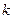 的取值范围。
的取值范围。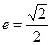 ,此椭圆与直线
,此椭圆与直线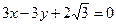 交于A、B两点,且OA⊥OB(其中O为坐标原点).
交于A、B两点,且OA⊥OB(其中O为坐标原点).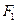 、
、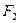 为椭圆的两个焦点,求
为椭圆的两个焦点,求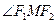 的取值范围;
的取值范围;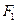 、
、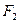 是椭圆
是椭圆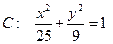 的两个焦点,
的两个焦点,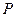 为椭圆上一点,且
为椭圆上一点,且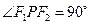 ,则
,则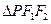 的面积 .
的面积 .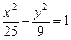 与椭圆
与椭圆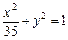 有相同的焦点;②“
有相同的焦点;②“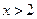 ”是“
”是“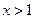 ”的必要不充分条件;③若
”的必要不充分条件;③若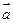 、
、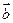 共线,则
共线,则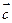 三
三 向量两两共面,则
向量两两共面,则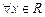 ,
,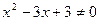 .
. 其中是真命题的有:_
其中是真命题的有:_  ___.(把你认为正确命题的序号都填上).
___.(把你认为正确命题的序号都填上).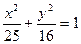 上的一点P,到椭圆一个焦点的距离为3,则P到另一焦点距离为 ( )
上的一点P,到椭圆一个焦点的距离为3,则P到另一焦点距离为 ( ) 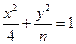 恒有两个交点,则
恒有两个交点,则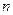 的取值范围____
的取值范围____