题目内容
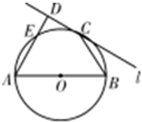如图，圆O的直径AB=8，C为圆周上一点，BC=4，过C作圆的切线l，过A作直线l的垂线AD，D为垂足，AD与圆O交于点E，则线段AE的长为考点：与圆有关的比例线段
专题：推理和证明
分析：连接OC，BE，由已知得△OBC为等边三角形，∠COB=60°，OC⊥直线l，AD∥OC，从而Rt△ABE中∠A=∠COB=60°，由此能求出AE．
解答：
解：连接OC，BE，如下图所示，
∵圆O的直径AB=8，BC=4，
∴△OBC为等边三角形，∠COB=60°
又∵直线l是过C的切线，故OC⊥直线l
又∵AD⊥直线l，∴AD∥OC，
故在Rt△ABE中∠A=∠COB=60°，
∴AE=
AB=4．
故答案为：4．
∵圆O的直径AB=8，BC=4，
∴△OBC为等边三角形，∠COB=60°
又∵直线l是过C的切线，故OC⊥直线l
又∵AD⊥直线l，∴AD∥OC，
故在Rt△ABE中∠A=∠COB=60°，
∴AE=
| 1 |
| 2 |
故答案为：4．
点评：本题考查与圆有关的线段长的求法，是中档题，解题时要认真审题，注意圆的简单性质的合理运用．
练习册系列答案
相关题目
某高校在今年的自主招生考试成绩中随机抽取100名考生的笔试成绩，分为5组制出频率分布直方图如图所示．若不等式|ax+1|≤3 的解集为{x|-2≤x≤1}．则a的值为（ ）
| A、2 | ||
| B、1 | ||
C、
| ||
| D、-2 |