题目内容
“a=0”是“函数f（x）=x2+ax在区间（0，+∞）上是增函数”的（ ）A．充分而不必要条件
B．必要而不充分条件
C．充分必要条件
D．既不充分也不必要条件
【答案】分析：函数f（x）=x2+ax在区间（0，+∞）上是增函数，结合二次函数的图象求出a的范围，再利用集合的包含关系判充要条件．
解答：解：函数f（x）=x2+ax在区间（0，+∞）上是增函数，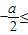
0，a≥0，“a=0”⇒“a≥0”，反之不成立．
故选A
点评：本题考查充要条件的判断，属基本题．
解答：解：函数f（x）=x2+ax在区间（0，+∞）上是增函数，
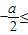0，a≥0，“a=0”⇒“a≥0”，反之不成立．故选A
点评：本题考查充要条件的判断，属基本题．
练习册系列答案
小学同步三练核心密卷系列答案
相关题目
“a=0”是“函数f（x）=x2+ax在区间（0，+∞）上是增函数”的（ ）
| A、充分而不必要条件 | B、必要而不充分条件 | C、充分必要条件 | D、既不充分也不必要条件 |
“a≥0”是“函数f（x）=|（ax-1）x|在区间（-∞，0）内单调递减”的（ ）
| A、充要条件 | B、必要不充分条件 | C、充分不f（x）=|（ax-1）x|必要条件 | D、即不充分也不必要条件 |