题目内容
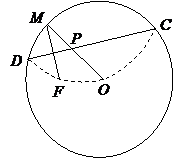
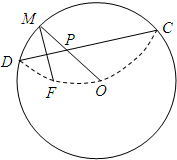一圆形纸片的半径为10cm，圆心为O，F为圆内一定点，OF=6cm，M为圆周上任意一点，把圆纸片折叠，使M与F重合，然后抹平纸片，这样就得到一条折痕CD，设CD与OM交于P点（如图），建立适当的直角坐标系，求点P的轨迹方程．分析：由于圆纸片折叠，折痕为CD，所以CD垂直平分线段MF，从而可知点P的轨迹是以F，O为焦点的椭圆，建立直角坐标系，可求轨迹方程．
解答：解：以FO所在直线为x轴，线段FO的中垂线为y轴，建立直角坐标系．
由题设，得：CD垂直平分线段MF，则有：|PO|+|PF|=|PO|+|PM|=|OM|=10
即|PO|+|PF|=10＞|OF|，所以点P的轨迹是以F，O为焦点的椭圆． 方程为：
+
=1，2a=10，2c=6⇒b2=16，点P的轨迹方程为：
+
=1；
由题设，得：CD垂直平分线段MF，则有：|PO|+|PF|=|PO|+|PM|=|OM|=10
即|PO|+|PF|=10＞|OF|，所以点P的轨迹是以F，O为焦点的椭圆． 方程为：
| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 25 |
| y2 |
| 16 |
点评：本题主要考查椭圆的定义，考查标准方程的求解，正确转化是解题的关键．
练习册系列答案
相关题目
张老师有天觉得很无聊，她把一张半径为1的圆形纸片在边长为a（a≥3）的正方形内任意移动，那么在正方形内，这张圆形纸片“不能接触到的部分”的面积是（ ）
