Question

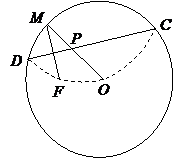
一圆形纸片的半径为10 cm，圆心为O，F为圆内一定点，OF＝6 cm，M为圆周上任意一点，把圆纸片折叠，使M与F重合，然后抹平纸片，这样就得到一条折痕CD，设CD与OM交于P点，如图

(1)求点P的轨迹方程；

(2)求证：直线CD为点P轨迹的切线．

Answer 1

答案：
解析：

(1)由题意知点M、F关于直线CD对称，可联想椭圆的定义求点P的轨迹；(2)可用反证法来证明．) 　　解：(1)由题意知点M、F关于直线CD对称，连结PF，则PF＝NF，故PF＋PO＝PO＋PM＝10＞6＝OF． 　　故点P的轨迹是以O、F为焦点、长轴长为10的椭圆． 　　以OF所在的直线为x轴，线段OF的中垂线为y轴建立 　　平面直角坐标系．易求得点P的方程为：　　8分 　　(2)假设CD不是点P轨迹的切线．则直线CD与椭圆一定相交． 　　设Q是CD上异于P的另一个交点， 　　则QF＋QO＝QM＋QO＞OM，这与点Q在椭圆上矛盾，假设不成立． 　　故直线CD与该椭圆切于点P　　14分