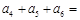题目内容
.(本小题共13分)函数 的定义域为R,数列
的定义域为R,数列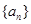 满足
满足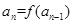 (
(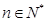 且
且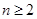 ).
).
(Ⅰ)若数列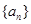 是等差数列,
是等差数列,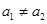 ,且
,且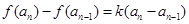 (k为非零常数,
(k为非零常数, 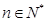 且
且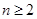 ),求k的值;
),求k的值;
(Ⅱ)若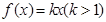 ,
,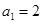 ,
,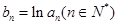 ,数列
,数列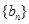 的前n项和为
的前n项和为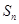 ,对于给定的正整数
,对于给定的正整数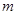 ,如果
,如果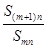 的值与n无关,求k的值.
的值与n无关,求k的值.
 的定义域为R,数列
的定义域为R,数列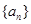 满足
满足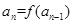 (
(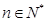 且
且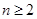 ).
).(Ⅰ)若数列
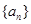 是等差数列,
是等差数列,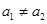 ,且
,且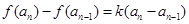 (k为非零常数,
(k为非零常数, 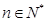 且
且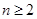 ),求k的值;
),求k的值;(Ⅱ)若
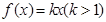 ,
,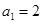 ,
,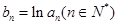 ,数列
,数列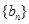 的前n项和为
的前n项和为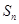 ,对于给定的正整数
,对于给定的正整数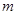 ,如果
,如果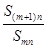 的值与n无关,求k的值.
的值与n无关,求k的值.解:(Ⅰ)当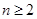 时,
时,
因为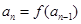 ,
,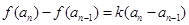 ,
,
所以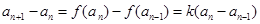 .
.
因为数列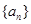 是等差数列,所以
是等差数列,所以 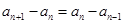 .
.
因为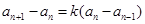 , 所以
, 所以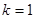 . ……………6分
. ……………6分
(Ⅱ)因为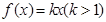 ,
,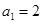 ,且
,且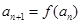 ,
,
所以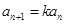 .
.
所以数列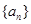 是首项为2,公比为
是首项为2,公比为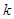 的等比数列,
的等比数列,
所以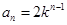 .
.
所以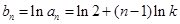 .
.
因为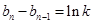 ,
,
所以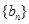 是首项为
是首项为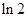 ,公差为
,公差为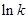 的等差数列.
的等差数列.
所以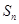
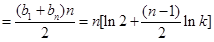 .
.
因为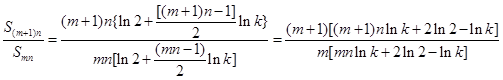 ,
,
又因为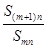 的值是一个与n无关的量,
的值是一个与n无关的量,
所以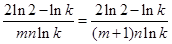 ,
,
解得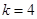 . ……………………13分
. ……………………13分
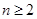 时,
时,因为
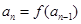 ,
,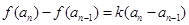 ,
,所以
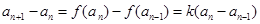 .
.因为数列
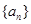 是等差数列,所以
是等差数列,所以 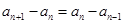 .
.因为
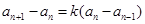 , 所以
, 所以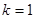 . ……………6分
. ……………6分(Ⅱ)因为
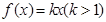 ,
,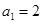 ,且
,且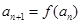 ,
,所以
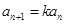 .
.所以数列
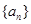 是首项为2,公比为
是首项为2,公比为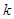 的等比数列,
的等比数列,所以
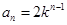 .
.所以
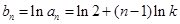 .
.因为
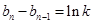 ,
,所以
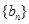 是首项为
是首项为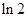 ,公差为
,公差为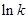 的等差数列.
的等差数列.所以
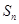
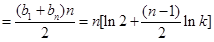 .
.因为
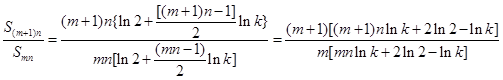 ,
,又因为
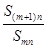 的值是一个与n无关的量,
的值是一个与n无关的量,所以
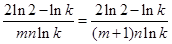 ,
,解得
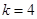 . ……………………13分
. ……………………13分略

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
相关题目
 n∈N*, Sn,Sn+1,Sn+2不构成等比数列.
n∈N*, Sn,Sn+1,Sn+2不构成等比数列. 的相邻两项
的相邻两项 是关于
是关于 的方程
的方程 的两根,且
的两根,且
 是等比数列;
是等比数列; 项和
项和 ;
; 对任意的
对任意的 都成立,求
都成立,求 的取值范围。
的取值范围。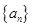 满足
满足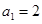 ,
,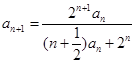 (
(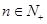 ).
).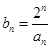 ,求数列
,求数列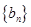 的通项公式
的通项公式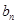 ;
;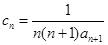 ,数列
,数列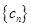 的前
的前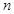 项和为
项和为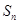 ,求
,求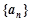 各项均为正数,其前
各项均为正数,其前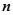 项和为
项和为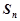 ,且满足
,且满足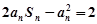 .
.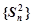 为等差数列,并求数列
为等差数列,并求数列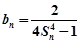 , 求数列
, 求数列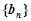 的前n项和
的前n项和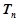 ,并求使
,并求使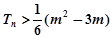 对所
对所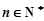 都成立的最大正整数m的值.
都成立的最大正整数m的值. 中
中 ,且满足
,且满足 则
则 的值为
的值为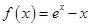 (
(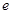 是自然对数的底数)
是自然对数的底数)
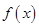 的最小值;
的最小值;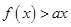 的解集为P, 若
的解集为P, 若
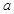 的取值范围;
的取值范围;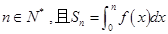 ,是否存在等差数列
,是否存在等差数列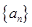 和首项为
和首项为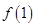 公比大于0的等比数列
公比大于0的等比数列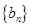 ,使数列
,使数列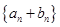 的前n项和等于
的前n项和等于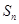
 的前
的前 项和
项和 ,对于任意的
,对于任意的 ,都满足
,都满足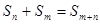 ,
,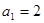 ,则
,则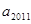 等于( )
等于( )

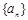 的前
的前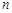 项和
项和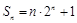 ,则
,则