题目内容
一动圆与圆O1∶(x-1)2+y2=1外切,与圆O2∶(x+1)2+y2=9内切.
(Ⅰ)求动圆圆心M的轨迹L的方程.
(Ⅱ)设过圆心O1的直线l∶x=my+1与轨迹L相交于A、B两点,请问△ABO2(O2为圆O2的圆心)的内切圆N的面积是否存在最大值?若存在,求出这个最大值及直线l的方程,若不存在,请说明理由.
答案:
解析:
解析:
|
解:(1)设动圆圆心为M(x,y),半径为R. 由题意,得 由椭圆定义知M在以O1,O2为焦点的椭圆上,且a=2,c=1, ∴动圆圆心M的轨迹L的方程为 (2)如图,设△ABO2内切圆N的半径为r,与直线l的切点为C,则三角形△ABO2的面积
当S△ABO2最大时,r也最大,△ABO2内切圆的面积也最大,(7分) 设 则 由 解得 有 当t≥1时, 即当t=1,m=0时,4r有最大值3,得 ∴存在直线 |

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目

 ,得
,得 ,令
,令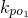 •
•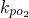 =1?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
=1?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).