题目内容
一动圆与圆O1:(x+3)2+y2=1外切,与圆O2:(x-3)2+y2=81内切,求动圆圆心的轨迹方程.
答案:
解析:
解析:
|
解:两定圆的圆心和半径分别是 O1(-3,0),r1=1,O2(3,0),r2=9,设动圆的圆心的坐标是M(x,y),半径为R,则由题可得|MO1|=1+R,|MO2|=9-R,∴|MO1|+|MO2|=10,由椭圆的定义知点M在以O1、O2为焦点的椭圆上,且2a=10,2c=6,∴a2=25,c2=9,b2=16,所以所求的圆心的轨迹方程是分析:两圆相切时,圆心之间的距离与两圆的半径有关,可以找到动圆圆心满足的条件. |

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
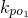 •
•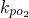 =1?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
=1?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).