题目内容
一动圆与圆O1:(x+2)2+y2=3外切,与圆O2:(x-2)2+y2=27内切.
(I)求动圆圆心M的轨迹方程;
(II)试探究圆心M的轨迹上是否存在点P,使直线与PO1的斜率kpo1•kpo2=1?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
(I)求动圆圆心M的轨迹方程;
(II)试探究圆心M的轨迹上是否存在点P,使直线与PO1的斜率kpo1•kpo2=1?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
分析:(1)设动圆圆心为M(x,y),半径为R.由题意,得|MO1|=
+R,|MO2|=3
-R,由椭圆定义知M在以O1,O2为焦点的椭圆上,由此能求出动圆圆心M的轨迹方程.
(II)由动圆圆心M的轨迹是椭圆,它的两个焦点坐标分别为O1(-2,0)和O2(2,0),设P(x,y)是椭圆上的点,由kPO1•kPO2=1,得
•
=1,(x≠±2),由此能够推导出圆心M的轨迹上存在四个点P,使直线PO1与PO2的斜率kPO1•kPO2=1.
| 3 |
| 3 |
(II)由动圆圆心M的轨迹是椭圆,它的两个焦点坐标分别为O1(-2,0)和O2(2,0),设P(x,y)是椭圆上的点,由kPO1•kPO2=1,得
| y |
| x+2 |
| y |
| x-2 |
解答:解:(1)设动圆圆心为M(x,y),半径为R.
由题意,得|MO1|=
+R,|MO2|=3
-R,(1分)
∴|MO1|+|MO2|=4
,
由椭圆定义知M在以O1,O2为焦点的椭圆上,(3分)
且a=2
,c=2,
∴b2=a2-c2=12-4=8. (5分)
∴动圆圆心M的轨迹方程为
+
=1. (6分)
(II)由(I)知动圆圆心M的轨迹是椭圆,
它的两个焦点坐标分别为O1(-2,0)和O2(2,0),(7分)
设P(x,y)是椭圆上的点,
由kPO1•kPO2=1,
得
•
=1,(x≠±2)(9分)
即x2-y2=4(x≠±2),这是实轴在x轴,顶点是椭圆的两个焦点的双曲线,
它与椭圆的交点即为点P.
由于双曲线的两个顶点在椭圆内,
根据椭圆和双曲线的对称性可知,它们必有四个交点.
即圆心M的轨迹上存在四个点P,
使直线PO1与PO2的斜率kPO1•kPO2=1.(12分)
由题意,得|MO1|=
| 3 |
| 3 |
∴|MO1|+|MO2|=4
| 3 |
由椭圆定义知M在以O1,O2为焦点的椭圆上,(3分)
且a=2
| 3 |
∴b2=a2-c2=12-4=8. (5分)
∴动圆圆心M的轨迹方程为
| x2 |
| 12 |
| y2 |
| 8 |
(II)由(I)知动圆圆心M的轨迹是椭圆,
它的两个焦点坐标分别为O1(-2,0)和O2(2,0),(7分)
设P(x,y)是椭圆上的点,
由kPO1•kPO2=1,
得
| y |
| x+2 |
| y |
| x-2 |
即x2-y2=4(x≠±2),这是实轴在x轴,顶点是椭圆的两个焦点的双曲线,
它与椭圆的交点即为点P.
由于双曲线的两个顶点在椭圆内,
根据椭圆和双曲线的对称性可知,它们必有四个交点.
即圆心M的轨迹上存在四个点P,
使直线PO1与PO2的斜率kPO1•kPO2=1.(12分)
点评:本题考查动圆圆心轨迹的求法,探索满足条件的点的存在性.考查运算求解能力,推理论证能力;考查化归与转化思想.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
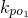 •
•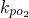 =1?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).
=1?若存在,请指出共有几个这样的点?并说明理由(不必具体求出这些点的坐标).