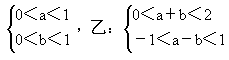下列四组条件中.甲是乙的充分不必要条件的是．( ) B．甲:ab＜0.乙:|a+b|＜|a-b| 题目和参考答案——青夏教育精英家教网—

题目内容

下列四组条件中，甲是乙的充分不必要条件的是．( )

B．甲：ab＜0，乙：|a+b|＜|a－b|

答案：
解析：

分析　如果不等式是关于自然数命题的形式，又无好的切入点时，不妨试用数学归纳法来证明．

证明:(1)当n=1时，左边=(a+b)－(a+b)=0，右边=2²－2²=0，所以左=右，因此原不等式成立．

(2)假设n=k时，不等式成立，即(a+b)^k－(a^k+b^k)≥2^2k－2^k⁺¹．则n=k+1

于是有ab=a+b≥4．因此

(a+b)^k⁺¹－(a^k⁺¹+b^k⁺¹)

=(a+b)(a+b)^k－(a+b)(a^k+b^k)+(a+b)(a^k+b^k)－(a^k⁺¹+b^k⁺¹)

=(a+b)[(a+b)^k－(a^k+b^k)]+(a^k⁺¹+b^k⁺¹)+ab^k+ba^k－(a^k⁺¹+b^k⁺¹)

所以n=k+1时，原不等式成立．

综合(1)，(2)，对于任意的自然数n，原不等式成立．

练习册系列答案

1加1阅读好卷系列答案

试题分类