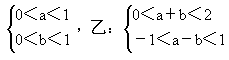Question

下列四组条件中，甲是乙的充分不必要条件的是（　　）

• A．甲  a＞b，乙  

  1

  a

  ＜

  1

  b

• B．甲  ab＜0，乙|a+b|＜|a-b|
• C．甲 

  0＜a＜1 0＜b＜1

  ，乙  

  0＜a+b＜2 -1＜a-b＜2

• D．甲  a=b，乙  a+b=2

  ab

Answer 1

分析：逐个验证：选项A，可取a=1，b=-2，可推翻结论；选项B，可得甲是乙的要条件；选项C，可得甲的充要条件为

0＜a+b＜2 -1＜a-b＜1

，由集合的包含关系可得；选项D，取a=b=-1，可推翻结论．

解答：解：选项A，可取a=1，b=-2，显然有

1

a

＞

1

b

，故由甲不能推出乙，故甲不是乙的充分不必要条件，故错误；
选项B，由|a+b|＜|a-b|平方可得a²+2ab+b²＜a²-2ab+b²，即ab＜0，故甲是乙的要条件，故错误；
选项C，由

0＜a＜1 0＜b＜1

两式相加可得0＜a+b＜2，还可得-1＜-b＜0，故-1＜a-b＜1，故甲的充要条件为

0＜a+b＜2 -1＜a-b＜1

，
而显然

0＜a+b＜2 -1＜a-b＜2

包含

0＜a+b＜2 -1＜a-b＜1

，故甲是乙的充分不必要条件，故正确；
选项D，取a=b=-1，则a+b=-2，但2

ab

=2，不甲不能推出乙，故甲不是乙的充分不必要条件，故错误．
故选C

点评：本题考查充要条件的判断，属基础题．