题目内容
(本题满分12分)
定义在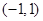 上的函数
上的函数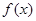 满足:①对任意
满足:①对任意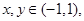 都有
都有 ;
;
②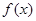 在
在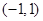 上是单调递增函数;③
上是单调递增函数;③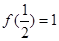 .
.
(Ⅰ)求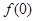 的值;
的值;
(Ⅱ)证明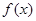 为奇函数;
为奇函数;
(Ⅲ)解不等式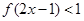 .
.
(Ⅰ) ;Ⅱ)定义域
;Ⅱ)定义域 关于原点对称 令
关于原点对称 令 ,则
,则 ,∴
,∴ 则
则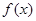 在
在 上为奇函数. (Ⅲ)
上为奇函数. (Ⅲ)
解析试题分析:(Ⅰ)取 ,则
,则 ,∴
,∴ 3分
3分
(Ⅱ)定义域 关于原点对称 4分
关于原点对称 4分
令 ,则
,则 ,
,
∴ 则
则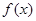 在
在 上为奇函数. 7分
上为奇函数. 7分
(Ⅲ)不等式可化为
∴解集为 12分
12分
考点:本题考查了抽象函数的性质
点评:一般地,抽象函数所满足的关系式,应看作给定的运算法则,则变量的赋值或变量及数值的分解与组合都应尽量与已知式或所给关系式及所求的结果相关联

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
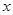 表示P点行程,
表示P点行程, 表PA的长,求
表PA的长,求
 是
是 的一个极值点
的一个极值点 的值;
的值; 的单调增区间;
的单调增区间; ,试问过点(2,5)可作多少条曲线y=g(x)的切线?为什么?
,试问过点(2,5)可作多少条曲线y=g(x)的切线?为什么? 有三个极值点。
有三个极值点。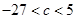 ;
;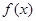 在区间
在区间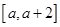 上单调递减,求
上单调递减,求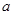 的取值范围。
的取值范围。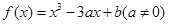 .
.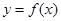 在点
在点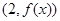 处与直线
处与直线 相切,求
相切,求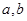 的值;
的值;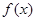 的单调区间与极值点.
的单调区间与极值点.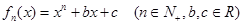
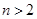 ,
,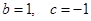 ,证明:
,证明: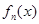 在区间
在区间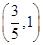 内存在唯一的零点;
内存在唯一的零点;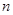 为偶数,
为偶数,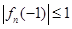 ,
,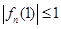 ,求
,求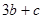 的最小值和最大值;
的最小值和最大值;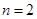 ,若对任意
,若对任意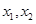
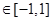 ,有
,有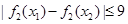 ,求
,求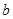 的取值范围;
的取值范围;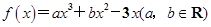 在点
在点 处的切线方程为
处的切线方程为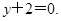
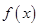 的解析式;
的解析式;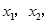 都有
都有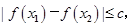 求实数c的最小值.
求实数c的最小值.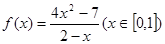
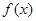 的单调区间和值域。
的单调区间和值域。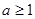 ,求函数
,求函数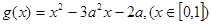 ,若对于任意
,若对于任意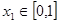 ,总存在
,总存在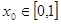 ,使得
,使得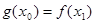 成立,求实数
成立,求实数 的取值范围。
的取值范围。