Question

某种平面分形图如下图所示，一级分形图是由一点出发的三条线段，长度均为1，两两夹角为120°；二级分形图是在一级分形图的每条线段的末端出发再生成两条长度为原来

1

3

的线段，且这两条线段与原线段两两夹角为120°；依此规律得到n级分形图．

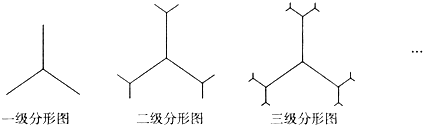
（I）n级分形图中共有

 

条线段；
（Ⅱ）n级分形图中所有线段长度之和为

 

．

Answer 1

考点：数列的应用

专题：综合题,等差数列与等比数列

分析：（I）n级分形图中的线段条数是以3为首项，2为公比的等比数列的和；
（Ⅱ）设n级分形图中所有线段的长度之和为a_n，先根据题意可得a₁、a₂、a₃、a₄的值，找到其中的关系，进而可得到数列的通项公式．

解答： 解：（I）n级分形图中的线段条数是以3为首项，2为公比的等比数列的和，即

3(1-2n)

1-2

=3•2ⁿ-3；
（Ⅱ）设n级分形图中所有线段的长度之和为a_n，依题意a₁=3，a₂=3+2×3×

1

3

=3+2，
a₃=3+2×3×

1

3

+2×2×3×(

1

3

)2=3+2+

4

3

，
…，
它们构成一个首项为3，公比为

2

3

的等比的和，
∴S_n=

3[1-( 2 3 )n]

1- 2 3

=9-9•(

2

3

)n．
故答案为：（Ⅰ）3•2ⁿ-3；（Ⅱ）9-9•(

2

3

)n．

点评：本题主要考查归纳推理，数列通项公式的求法．数列的通项公式在数列学习中占据很重要的地位，要强化学习．