题目内容
12.如图①,有一个长方体形状的敞口玻璃容器,底面是边长为20cm的正方形,高为30cm,内有20cm深的溶液.现将此容器倾斜一定角度α(图②),且倾斜时底面的一条棱始终在桌面上(图①、②均为容器的纵截面).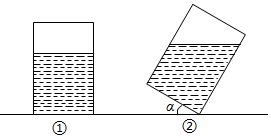
(1)要使倾斜后容器内的溶液不会溢出,角α的最大值是多少;
(2)现需要倒出不少于3000cm3的溶液,当α=60°时,能实现要求吗?请说明理由.
分析 (1)根据题意画出图形,结合图形,过C作CF∥BP,交AD所在直线于F,且点F在线段AD上,用tanα表示出DF、AF,求出容器内溶液的体积,列出不等式求出溶液不会溢出时α的最大值;
(2)当α=60°时,过C作CF∥BP,交AB所在直线于F,则点F在线段AB上,溶液纵截面为Rt△CBF,由此能求出倒出的溶液量,即可得出结论.
解答 解:(1)根据题意,画出图形,如图a所示,
过C作CF∥BP,交AD所在直线于F,
在Rt△CDF中,∠FCD=α,CD=20cm,DF=20tanα,
且点F在线段AD上,AF=30-20tanα,
此时容器内能容纳的溶液量为:
S梯形ABCF•20=$\frac{(AF+BC)•AB}{2}$•20
=(30-20tanα+30)•20•10
=2000(6-2tanα)(cm3);
而容器中原有溶液量为20×20×20=8000(cm3),
令2000(6-2tanα)≥8000,
解得tanα≤1,
所以α≤45°,
即α的最大角为45°时,溶液不会溢出;
(2)如图b所示,当α=60°时,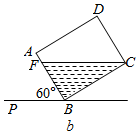
过C作CF∥BP,交AB所在直线于F,
在Rt△CBF中,BC=30cm,∠BCF=30°,BF=10$\sqrt{3}$cm,
∴点F在线段AB上,故溶液纵截面为Rt△CBF,
∵S△ABF=$\frac{1}{2}$BC•BF=150$\sqrt{3}$cm2,
容器内溶液量为150$\sqrt{3}$×20=3000$\sqrt{3}$cm3,
倒出的溶液量为(8000-3000$\sqrt{3}$)cm3<3000cm3,
∴不能实现要求.
点评 本题考查了棱柱的体积在生产生活中的实际应用问题,解题时要认真审题,注意空间思维能力的培养,是综合性题目.

练习册系列答案
相关题目
17.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F,若过点F且倾斜角为30°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是( )
| A. | ($\frac{1}{2}$,$\frac{2\sqrt{3}}{3}$) | B. | [$\frac{1}{2}$,$\frac{2\sqrt{3}}{3}$] | C. | ($\frac{\sqrt{3}}{3}$,+∞) | D. | [$\frac{2\sqrt{3}}{3}$,+∞) |
4.若双曲线$\frac{{x}^{2}}{3}$-$\frac{6{y}^{2}}{{p}^{2}}$=1的一个焦点与抛物线y2=2px的焦点重合,则该双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{6}$ | C. | 3 | D. | 2$\sqrt{3}$ |
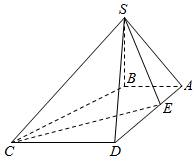 如图,在四棱锥S-ABCD中,SB⊥底面ABCD,底面ABCD为梯形,AB⊥AD,AB∥CD,AB=1,AD=3,CD=2.若点E是线段AD上的动点,则满足∠SEC=90°的点E的个数是( )
如图,在四棱锥S-ABCD中,SB⊥底面ABCD,底面ABCD为梯形,AB⊥AD,AB∥CD,AB=1,AD=3,CD=2.若点E是线段AD上的动点,则满足∠SEC=90°的点E的个数是( )