题目内容
7.设直线l与抛物线y2=4x相交于A,B两点,与圆 (x-5)2+y2=9相切于点M,且M为线段AB中点,则这样的直线l有( )条.| A. | 2 | B. | 3 | C. | 4 | D. | 无数条 |
分析 先确定M的轨迹是直线x=3,直线与圆有两个交点,直线l有两条;斜率不存在时,直线l有2条,即可得出结论.
解答 解:设A(x1,y1),B(x2,y2),M(x0,y0),
斜率存在时,设斜率为k,则y12=4x1,y22=4x2,
相减得(y1+y2)(y1-y2)=4(x1-x2),
当l的斜率存在时,利用点差法可得ky0=2,
因为直线与圆相切,所以$\frac{{y}_{0}}{{x}_{0}-5}$=-$\frac{1}{k}$,所以x0=3,
即M的轨迹是直线x=3.
圆心(5,0)到直线的距离为2<3,直线与圆有两个交点,直线l有两条;
斜率不存在时,直线l有2条;
所以直线l恰有4条,
故选:C.
点评 本题考查直线与抛物线、圆的位置关系,考查点差法,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
17.函数f(x)=$\frac{2}{x}$-log3x的零点所在的一个区间是( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
12.在四面体ABCD中,E、G分别是CD、BE的中点,若$\overrightarrow{AG}$=x$\overrightarrow{AB}$+y$\overrightarrow{AD}$+z$\overrightarrow{AC}$,则x+y+z=( )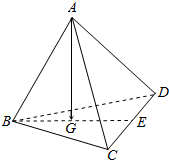

| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
19.已知a,b为非零实数,且a<b,则下列结论一定成立的是( )
| A. | a2<b2 | B. | a3<b3 | C. | $\frac{1}{a}$>$\frac{1}{b}$ | D. | ac2<bc2 |
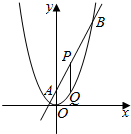 已知抛物线C:x2=2py(p>0)的焦点为F,直线l:y=2x+2交抛物线C于A,B两点,P是线段AB的中点,过P作x轴的垂直交抛物线C于点Q.
已知抛物线C:x2=2py(p>0)的焦点为F,直线l:y=2x+2交抛物线C于A,B两点,P是线段AB的中点,过P作x轴的垂直交抛物线C于点Q.
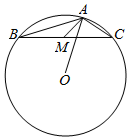 已知△ABC外接圆的圆心为O,$AB=2\sqrt{3}$,$AC=2\sqrt{2}$,A为钝角,M是BC边的中点,则$\overrightarrow{AM}•\overrightarrow{AO}$=( )
已知△ABC外接圆的圆心为O,$AB=2\sqrt{3}$,$AC=2\sqrt{2}$,A为钝角,M是BC边的中点,则$\overrightarrow{AM}•\overrightarrow{AO}$=( )