题目内容
14．
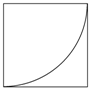一块正方形薄铁片的边长为4cm，以它的一个顶点为圆心，一边长为半径画弧，沿弧剪下一个扇形（如图），用这块扇形铁片围成一个圆锥筒，则这个圆锥筒的容积等于$\frac{\sqrt{15}}{3}$πcm3．
分析 设圆锥的底面圆的半径为r，根据圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长得到$\frac{90•π•4}{180}$=2πr，解得r=1，然后根据勾股定理计算圆锥的高．即可求解几何体的体积．
解答 解：设圆锥的底面圆的半径为r，
根据题意得 $\frac{90•π•4}{180}$=2πr，解得r=1，
所以这个圆锥的高=$\sqrt{{4}^{2}-{1}^{2}}$=$\sqrt{15}$（cm）．
圆锥的体积为：$\frac{1}{3}•π•{1}^{2}•\sqrt{15}$=$\frac{\sqrt{15}}{3}$π．cm3．
故答案为：$\frac{\sqrt{15}}{3}$π．
点评 本题考查了圆锥的计算：圆锥的侧面展开图为一扇形，这个扇形的弧长等于圆锥底面的周长，扇形的半径等于圆锥的母线长．
练习册系列答案
相关题目
5．若a＜b，d＜c，且（c-a）（c-b）＜0，（d-a）（d-b）＞0，则a，b，c，d大小关系是（ ）
| A． | d＜a＜c＜b | B． | d＜c＜a＜b | C． | a＜d＜b＜c | D． | a＜d＜c＜b |
6．把函数y=cos（2x+φ）（|φ|＜$\frac{π}{2}$）的图象向左平移$\frac{π}{6}$个单位，得到函数y=f（x）的图象关于直线x=$\frac{5π}{12}$对称，则φ的值为（ ）
| A． | -$\frac{π}{12}$ | B． | -$\frac{π}{6}$ | C． | $\frac{π}{6}$ | D． | $\frac{π}{12}$ |
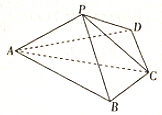如图，四棱锥P-ABCD中，平面PAC⊥底面ABCD，BC=CD=$\frac{1}{2}$AC=2，∠ACB=∠ACD=$\frac{π}{3}$．