题目内容
14．已知数列{an}满足a1=2，an+1=3an+2（n∈N*）（1）求证：数列{an+1}是等比数列；
（2）求数列{an}的通项公式an与前n项和Sn．
分析 （1）由an+1=3an+2（n∈N*），变形为an+1+1=3（an+1），即可证明；
（2）利用等比数列的前n项和公式即可得出．
解答 （1）证明：∵a1=2，an+1=3an+2（n∈N*），
∴an+1+1=3（an+1），
∴数列{an+1}是等比数列，首项为3，公比为3．
（2）解：由（1）可得：an+1=3n，解得an=3n-1．
Sn=$\frac{3（{3}^{n}-1）}{3-1}$-n=$\frac{{3}^{n+1}}{2}$-$\frac{3}{2}$-n．
点评 本题考查了递推关系、等比数列的通项公式及其前n项和公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
4．
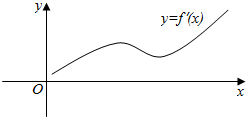定义在全体正实数上的函数f（4）=1，f′（x）为f（x）的导函数，已知函数y=f′（x）的图象如图所示lnb≥ln2a且f（2a+b）≥1，则$\frac{3b+6}{2a+4}$的取值范围是（ ）
定义在全体正实数上的函数f（4）=1，f′（x）为f（x）的导函数，已知函数y=f′（x）的图象如图所示lnb≥ln2a且f（2a+b）≥1，则$\frac{3b+6}{2a+4}$的取值范围是（ ）| A． | [1，+∞] | B． | [2，+∞] | C． | [$\frac{3}{4}$，2] | D． | [0，3] |
2．下列各式恒成立的是（ ）
| A． | tan$\frac{α}{2}$=$\frac{1-cosα}{sinα}$ | B． | $\frac{1+cos2α}{2}$=cos2α | ||
| C． | $\frac{2tan\frac{α}{2}}{1-ta{n}^{2}\frac{α}{2}}$=tanα | D． | ±$\sqrt{\frac{1-cosα}{1+cosα}}$=tan$\frac{α}{2}$ |
9．已知函数f（x）=$\frac{x}{|x-1|}$，g（x）=1+$\frac{x+|x|}{2}$，若f（x）＜g（x），则实数x的取值范围是（ ）
| A． | （-∞，$\frac{-1-\sqrt{5}}{2}$）∪（$\frac{-1+\sqrt{5}}{2}$，+∞） | B． | （-∞，$\frac{-1-\sqrt{5}}{2}$）∪（$\frac{1+\sqrt{5}}{2}$，+∞） | ||
| C． | （$\frac{-1+\sqrt{5}}{2}$，$\frac{1+\sqrt{5}}{2}$） | D． | （$\frac{-1+\sqrt{5}}{2}$，1）∪（1，$\frac{1+\sqrt{5}}{2}$） |
19．下列函数f（x）与g（x）是相同函数的是（ ）
| A． | f（x）=$\frac{x-1}{{x}^{2}-1}$，g（x）=$\frac{1}{1+x}$ | B． | f（x）=（$\sqrt{x}$）2，g（x）=$\sqrt{{x}^{2}}$ | ||
| C． | f（x）=$\root{3}{{x}^{4}-{x}^{3}}$，g（x）=x$\root{3}{x-1}$ | D． | f（x）=1，g（x）=sin（arcsinx） |