题目内容
直三棱柱 中,
中,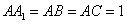 ,
,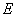 ,
,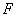
分别是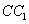 、
、 的中点,
的中点,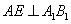 ,
, 为棱
为棱 上的点.
上的点.
(1)证明: ;
;
(2)是否存在一点 ,使得平面
,使得平面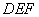 与平面
与平面 所成锐二面角的余弦值为
所成锐二面角的余弦值为 ?若存在,说明点D的位置,若不存在,说明理由.
?若存在,说明点D的位置,若不存在,说明理由.

 1)证明:
1)证明: ,
, ∥
∥
 又
又

 面
面 又
又 面
面
 ………2分
………2分
以 为原点建立如图所示的空间直角坐标系
为原点建立如图所示的空间直角坐标系 
则 ,
, ,
, ,
, ,
,
设 ,
, 且
且 ,
,
即:


 ………5分
………5分


 ………6分
………6分
(2)假设存在,设面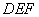 的法向量为
的法向量为  ,
,
则 


 即:
即:  令
令
 . ………8分
. ………8分
由题可知面 的法向量
的法向量 ………9分
………9分
 平面
平面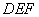 与平面
与平面 所成锐二面的余弦值为
所成锐二面的余弦值为
 即:
即:
 或
或 (舍) ………11分
(舍) ………11分
 当点
当点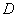 为
为 中点时,满足要求. ………12分
中点时,满足要求. ………12分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如右数据:
| 单价 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量 | 90 | 84 | 83 | 80 | 75 | 68 |
由表中数据,求得线性回归方程为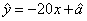 .若在这些样本点中任取一点,则它在回归直线左下方的概率为_______.
.若在这些样本点中任取一点,则它在回归直线左下方的概率为_______.
 }中,
}中, 求{
求{ .
.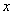 (元)
(元) (件)
(件) 的值为
的值为 D.
D.

 ~
~ ,若
,若 ,则
,则 ____________.
____________.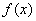 =
= .
.  的解集;
的解集; 对任意实数
对任意实数 恒成立,求实数
恒成立,求实数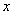 的取值范围.
的取值范围. ,则△ABC的面积为
,则△ABC的面积为
 的解集;(Ⅱ)证明:
的解集;(Ⅱ)证明: 
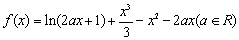 .
. ,判断
,判断 的单调性.
的单调性. 在
在 上为增函数,求实数
上为增函数,求实数 的取值范围;
的取值范围; 时,方程
时,方程 有实根,求实数
有实根,求实数 的最大值.
的最大值.